Exo Méca PCSI

[xPingoo]

Bonjour à tous, j'ai un problème pour résoudre un exercice de mécanique.
Voici le sujet :

Un adepte du roller assimilé à un point matériel M de masse m, se lâche sans vitesse initiale depuis le point A d'une rampe, située à la hauteur h au dessus de O, point le plus bas de la rampe.
A partir de O, la rampe a une forme cylindrique de rayon r. Le patineur peut rouler à l'intérieur de ce cylindre en restant dans le plan vertical (Oxy) et éventuellement faire le tour complet. Le contact est sans frottement sur toute la surface.

1) Montrer que la norme vo de la vitesse du patineur au point O sécrit : vo = (2gh)^1/2
Je pense avoir réussi cette question, j'ai trouvé le bon résultat en appliquant le théorème de l'énergie cinétique entre A et O

2) Déterminer la norme v de la vitesse du patineur en un point M quelconque du cylindre, repéré par l'angle Teta, en fonction de g, h, r et Teta
Ici, j'applique le théorème de l'énergie cinétique entre O et un point quelconque M et j'arrive à vm=[2g(h+r cosTeta sinTeta)]^1/2 ce qui ne me semble pas bon.. Pourriez vous m'aider svp?

3) En appliquant le théorème adéquate, montrer que la réaction exercée par le supprt cylindrique sur le patineur est :
N=mg(2h/r + 3cosTeta - 2)
En appliquant le Principe Fondamental de la Dynamique j'arrive à N=mg(3cosTeta - 2).. Je ne vois pas d'où vient le "2h/r". Là encore j'aurais besoin de votre aide.

Merci d'avance!

[Arnaud-29-31]

Salut,

Il aurait été bien de mettre un schéma, ici l'angle est pris avec quelle origine ?
Sinon pour la 2, effectivement il y a un problème, je vois mal comment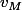 peut être supérieure à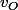

Vue l'expression proposée pour N, l'origine doit être telle que \theta = 0 lorsque M est en O

Le théorème de l'énergie cinétique donne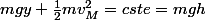
Que vaut y en fonction de r et ?

Pour la dernière question, le PFD projeté sur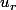 et 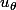donne bien le résultat.

[xPingoo]

Oui, teta est l'angle entre les vecteurs (CO;CM) avec C le centre du cercle.

J'ai trouvé que x(O)-x(M) = r sin Teta, que j'ai inclu dans mon théorème de l'énergie cinétique entre O et M, c'est ça qui est sûrement faux à mon avis..

[Arnaud-29-31]

x(M) - x(O) ca fait bien r.sin( mais c'est y(M) - y(O) que l'on veut.

[xPingoo]

y(M) - y(O)? Je ne comprends pas bien..
Voilà ce que j'ai fait en fait :
Travail élémentaire de P = mg cosTeta dx
Du coup, le travail de P = mg cosTeta (x(M) - x(O)) en intégrant

ce n'est pas ce que nous voulons? S' il faut chercher selon dy, dans ce cas on aurait P = -mg sin Teta (y(M)-y(O)) non?
[Puisque les coordonnées de P sont (mg cosTeta; -mg sinTeta; 0)]

[xPingoo]

Voici le schéma, je n'ai pas réussi à faire mieux, désolée..

[Arnaud-29-31]

Je jurerais que le poids est suivant et non pas suivant ...

Tu as pourtant bien réussis à exprimer le travail entre A et O qui valait mgh ...

[xPingoo]

Oh oui bien sûr, il est suivant ey.. Quelle erreur! :doh:
Mais le travail du poids ne s'annule pas puisque OM et P ne sont pas colinéaires..
P = -mg sinTeta (y(M)-y(O)) serait la solution?

[Arnaud-29-31]

Tu voulait écrire W(P) à la place de P ?
Non ce n'est pas ça ...

[xPingoo]

W(P) oui.. Bon bah j'ai plus qu'à recommencer! :)

[xPingoo]

J'arrive à W(P)= -mg sinTeta r(1-cosTeta)
En remplacement y(M) = -r cosTeta et y(O)= -r

[Mathusalem]

Je ne comprends pas bien la difficulté :

Tu connais la vitesse initiale du patineur lorsqu'il arrive dans le looping, au point O. Tu l'as calculée en 1).

Ensuite, tu saisq que le problème est libre de friction, et que tu peux appliquer le théorème de conservation d'énergie sans autre.

Alors, tu connais la vitesse initiale en O. Tu peux considérer que ceci définit ta hauteur nulle. Ensuite, le tout est d'utiliser
1/2 mvinitial^2 + mg0 = 1/2mv^2 + mgHauteurDansLooping.

La finesse est d'exprimer la hauteur dans le looping, qui est R(1 - cos(teta)) selon ton dessin. Tu isoles v et t'es champion.

Pour la 3), tu connais la vitesse du patineur dans le cylindre en n'importe quel point du cylindre (suffit de connaître theta).

Qu'est-ce qui relie une vitesse tangentielle forcée à se mouvoir sur un cercle à une force qui l'obligerait à se mouvoir sur un cercle ?

[Mathusalem]

Peux-tu faire voir tes calculs ?
J'arrive à la réponse donnée en 3) à la différence que j'ai un 2 devant le cos(teta).

Peut-être j'ai mal compris l'énoncé ?

[Mathusalem]

Ah c'est bon j'ai compris !

Bon :

1)


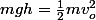
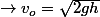
2) Connaissant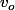 à l'entrée du looping, on cherche à savoir la différence d'atltitude à l'intérieur du looping en fonction de R et de .
Notons h' la hauteur dans le looping, alors on a


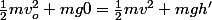
h' peut se décrire comme

Je te laisse calculer v.

3)
On contraint une vitesse v à se mouvoir de manière circulaire. l'accélération requise pour le faire est une accélération centrale de norme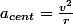 avec r le rayon du cercle désiré.

Ainsi, sur le support s'exerce , avec la composante normale au cercle de la gravitation.

On arrive au résultat demandé.

[Arnaud-29-31]

J'arrive à W(P)= -mg sinTeta r(1-cosTeta)
En remplacement y(M) = -r cosTeta et y(O)= -r

Comme tu as l'air maintenant de l'avoir trouvé, y(M) vaut bien mais je ne comprends pas pourquoi tu t'obstines à rajouter
Il faut que tu revois les bases sur le travail d'une force : comment ca se calcul et les propriétés tel que "le travail ne dépend pas du chemin suivit".


Ici le poids est suivant ,
(avec H le projeté de M sur (Ox), j'utilise le fait que le travail ne dépend pas du chemin suivit)
D'où au final,

[Mathusalem]

j'utilise le fait que le travail ne dépend pas du chemin suivit)

précisons que cela est valable pour une force conservative, telle que le poids.
Ce n'est pas valable pour n'importe quel type de force.

L'argument "instinct", pour xPingoo est le suivant :

l'energie potentielle mgh est le travail de la gravité, qui ne dépend que de la différence verticale (..) de position.

En effet, si tu bouges une masse dans un plan horizontal, et que tu la lâches, la vitesse qu'elle peut "potentiellement" atteindre est indépendant d'où tu te situes dans le plan. Or, si tu la mets un peu plus haut, elle atteindra une vitesse plus grande (donc l'énergie potentielle est plus grande).

Après t'utilises le formalisme proposé par Arnaud pour faire les trucs concrets, mais faut aussi 'sentir' la physique

[xPingoo]

h' peut se décrire comme

Pouvez-vous m'expliquer comment vous arriver à cela? J'ai essayé de chercher sur le dessin une relation, mais je n'ai pas réussi..

Mais pour v j'ai trouvé v=[2g(h-r(1-cos(\theta))]^1/2

[xPingoo]

mais je ne comprends pas pourquoi tu t'obstines à rajouter

J'ai un sin(\theta) car pour moi, les coordonnées de P sont (mgcos(theta) ; -mgsin(theta) ; 0), selon (x;y;z)
Donc je calcule d'abord le travail élémentaire, P scalaire dOM (en vecteur)
Travail élém P = -mg sin(theta) dy
Et ensuite W(P) = -mg sin(theta) r(1-cos(theta))

PS : Désolée pour l'écriture, mais je ne connais pas les combines pour les symboles mathématiques.

[xPingoo]

Oh mais je crois que je viens de comprendre encore une mes erreurs (très bétes soit dit en passant..)
C'est par ce qu'en fait les coordonnées de mon vecteur P, je les obtiens en projetant P sur les vecteurs (er;e(theta); ez), dans ma base polaire, sur le petit schéma que j'ai fait..
Vraiment n'importe quoi, excusez-moi pour ça..

[xPingoo]

Par contre pour la question 3, voilà comment j'ai fait.. :
J'applique le Principe Fondamentale de la Dynamique dans la base polaire (avec le vecteur e(theta) orienté dans le sens du mouvement)
En projetant sur "er" j'ai :
N= mr(Theta"point")^2 + mg cos(Theta)
[ mr(Theta"point")^2 est la coordonnée de l'accélération suivant "er"]
Ensuite je cherche (Theta"point")^2 grâce au théorème du moment cinétique
J'arrive à (Teta"point")^2= (2g(1-cosTeta))/r
Ensuite je remplace dans l'expression de N, et j'arrive à N=mg(3cosTeta - 2)
On avait fait un exercice plus ou moins similaire en TD et on avait fait comme ça donc bon.. Mais il n'y a pas le "2h/r" dans l'expression que j'ai trouvé... Et je ne vois pas où je me suis trompée