Equivalences entre deux équations

[FunkyAnts]

Bonjour,

J'ai reçu le corrigé d'un devoir de Physique, et parfois j'ai du mal à suivre le raisonnement du prof quand il prend des raccourcis dans les équivalences. Pouvez-vous m'aider svp à combler les trous.

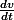
De m+ kv = mg

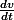
à ()/v = - dt

[Sa Majesté]

Il ne manque rien ?
Ça semble difficile de faire disparaître g comme ça

[Skullkid]

Bonsoir, comme le dit Sa Majesté c'est assez décousu tel quel (et la deuxième équation est inhomogène mais on va dire que c'est une coquille). Cela dit mes pouvoirs de médium me suggèrent quelque chose comme :

On veut résoudre (E) : mdv/dt + kv = mg. C'est une équation différentielle linéaire donc on sait que la solution générale de (E) est la somme d'une solution particulière de (E) et de la solution générale de l'équation sans second membre associée (E0) : mdv/dt + kv = 0. Donc on cherche d'abord à résoudre (E0), qu'on réécrit en dv/v = -kdt/m.

[FunkyAnts]

Merci Skullkid, c'était exactement ça.

Est-ce que je peux t'embêter encore un peu ?

Y a aussi la relation qui suit dans le raisonnement :

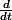
(ln v)=-

En intégrant cette relation, on obtient la solution générale

v=A exp(-t)


Cela doit vous paraître un peu neuneu, mais je ne voudrais pas laisser un doute.

Ps: je suis en reprise d'études, d'où de sérieux trous de mémoire.

[Sa Majesté]

Y a aussi la relation qui suit dans le raisonnement :

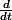
(ln v)=-

En intégrant cette relation, on obtient la solution générale

v=A exp(-t)

En fait tu peux réécrire l'équation écrite par Skullkid dv/v = -kdt/m en v'/v = -k/m
Et comme la dérivée de ln(v) est v'/v, tu obtiens =-
Puis tu intègres entre 0 et l'instant courant : ln(v/v0) = -kt/m, d'où v=v0 e^(-kt/m)

[FunkyAnts]

Merci Sa Majesté,

je vois bien qu'il faut utiliser l'expo pour enlever le ln et trouver v, mais l'intégration en 0 m'échappe.

Est-ce que tu peux détailler un peu plus stp.

[Sa Majesté]

Tu as =-

En intégrant entre 0 et l'instant courant : ln(v(t)) - ln(v(0)) = -kt/m

Et donc ln(v(t)/v(0)) = -kt/m

J'espère que c'est plus clair comme ça :lol3:

[FunkyAnts]

Merci Sa Majesté. :happy: