Approche à la méca Q

[Kikoo <3 Bieber]

Ah oui, je suis bête !! ^^ Je l'avais pensé en plus que la surface est orientée

Donc je vais essayer de donner quelque chose, merci pour ton aide Math ;)

[Kikoo <3 Bieber]

Poquito problem :

Je me retrouve avec

Mais quand j'intègre la première intégrale, ça me fait du plus l'infini, je vois pas le bleme... :/

[Mathusalem]

Poquito problem :

Je me retrouve avec

Mais quand j'intègre la première intégrale, ça me fait du plus l'infini, je vois pas le bleme... :/

Attention, theta va 0 a pi/2. Phi va de 0 a 2phi.

On n'a jamais dit que c'est censé converger en tous cas Je pourrais réfléchir physiquement à pourquoi ça converge pas, mais fatigué.Une autre fois

Regarde ce qu'il se passe si tu négliges 1 devant exp^(x). L'autre limite

Sinon, regarde sur wiki tu peux trouver le calcul exact (un peu chaud quand même) pour trouver la valeur de l'intégrale ( pas sa primitive )

[Skullkid]

exp(x) = 1+x c'est valable quand x est petit. Mais ici tu cherches à intégrer pour x allant de 0 à l'infini donc c'est normal que ça ne marche pas. Même souci pour x grand si tu dis que exp(x)-1 = exp(x). Au mieux tu peux obtenir un ordre d'idées en coupant l'intégrale en 2, genre [0,A] et [A,+l'infini[, et en appliquant tes approximations sur chacun des deux intervalles.

Mais bon, je préfère faire un changement de variable pour sortir le T de l'exponentielle. Tu te retrouves avec une constante fois T^4 fois l'intégrale de 0 à l'infini de x^3/(exp(x)-1)dx. Le fait de savoir que cette intégrale converge suffit à prouver la loi de Stefan-Boltzmann. En calculant l'intégrale explicitement on obtient l'expression de la constante de Stefan-Boltzmann en fonction des constantes fondamentales, mais c'est du bonus.

[Kikoo <3 Bieber]

Attention, theta va 0 a pi/2. Phi va de 0 a 2phi.

On n'a jamais dit que c'est censé converger en tous cas Je pourrais réfléchir physiquement à pourquoi ça converge pas, mais fatigué.Une autre fois

Regarde ce qu'il se passe si tu négliges 1 devant exp^(x). L'autre limite

Sinon, regarde sur wiki tu peux trouver le calcul exact (un peu chaud quand même) pour trouver la valeur de l'intégrale ( pas sa primitive )

Oui, j'ai confondu les deux !!

Sinon, pour l'autre intégrale entre 0 et l'infini, ils donnent 1, et ma calto donne 6,49394. Ca me donne envie de rire doucement...

PS : ok pour l'approximation abusive, Skull

[Kikoo <3 Bieber]

exp(x) = 1+x c'est valable quand x est petit. Mais ici tu cherches à intégrer pour x allant de 0 à l'infini donc c'est normal que ça ne marche pas. Même souci pour x grand si tu dis que exp(x)-1 = exp(x). Au mieux tu peux obtenir un ordre d'idées en coupant l'intégrale en 2, genre [0,A] et [A,+l'infini[, et en appliquant tes approximations sur chacun des deux intervalles.

Mais bon, je préfère faire un changement de variable pour sortir le T de l'exponentielle. Tu te retrouves avec une constante fois T^4 fois l'intégrale de 0 à l'infini de x^3/(exp(x)-1)dx. Le fait de savoir que cette intégrale converge suffit à prouver la loi de Stefan-Boltzmann. En calculant l'intégrale explicitement on obtient l'expression de la constante de Stefan-Boltzmann en fonction des constantes fondamentales, mais c'est du bonus.

Salut Skullkid !

Je peux essayer un dvpt en éléments simples ?

Edit : Mouais non ça marchera pas.
Je ne sais pas faire les changements de variable. Je verrai demain.
En tout cas c'est gentil de vous être occupé de mon problème aujourd'hui

[Kikoo <3 Bieber]

Poquito problem :

Je me retrouve avec

Mais quand j'intègre la première intégrale, ça me fait du plus l'infini, je vois pas le bleme... :/

J'ai vu la méthode avec les résidus... et... franchement... voilà ^^

Bon, je vais essayer d'avancer un peu le calcul d'une autre manière :



Et là j'appelle au secours !! En fait j'ai pas bien saisi ton approximation du "on néglige le 1 devant l'exp", mathusalem ^^

[Skullkid]

Il te manque un pi au numérateur. Une fois que tu es là, fais un changement de variable. Tu m'as dit que tu n'avais pas encore vu ça en cours, alors présentons-le à la physicienne : on a envie de poser x = h*nu/kT pour avoir un truc "simple" dans l'exponentielle. Pour que nu prenne toutes les valeurs de 0 à l'infini, x doit aussi prendre toutes les valeurs de 0 à l'infini. De plus, nu = kTx/h et dnu = kT*dx/h (une petite variation dx de x correspond à une variation dnu = kT*dx/h de nu). Le changement de variable ça consiste en gros à remplacer les bornes en nu par les bornes correspondantes en x, à exprimer tous les nu en fonction de x et le dnu en fonction de dx. Dans note cas :



Et le T^4 apparaît, avec une constante devant. En physique, on fait toujours les changements de variable comme ça, mais je te déconseille fortement d'écrire des trucs du genre dx = a*dy quand tu fais de "vraies" maths. Tu ne devrais pas tarder à voir le changement de variable "propre" en maths.

[Kikoo <3 Bieber]

Il te manque un pi au numérateur. Une fois que tu es là, fais un changement de variable. Tu m'as dit que tu n'avais pas encore vu ça en cours, alors présentons-le à la physicienne : on a envie de poser x = h*nu/kT pour avoir un truc "simple" dans l'exponentielle. Pour que nu prenne toutes les valeurs de 0 à l'infini, x doit aussi prendre toutes les valeurs de 0 à l'infini. De plus, nu = kTx/h et dnu = kT*dx/h (une petite variation dx de x correspond à une variation dnu = kT*dx/h de nu). Le changement de variable ça consiste en gros à remplacer les bornes en nu par les bornes correspondantes en x, à exprimer tous les nu en fonction de x et le dnu en fonction de dx. Dans note cas :



Et le T^4 apparaît, avec une constante devant. En physique, on fait toujours les changements de variable comme ça, mais je te déconseille fortement d'écrire des trucs du genre dx = a*dy quand tu fais de "vraies" maths. Tu ne devrais pas tarder à voir le changement de variable "propre" en maths.

D'accord, je vois
Et en ce qui concerne cette intégrale, je fais l'impasse !

[Kikoo <3 Bieber]

Bonjour, j'ai deux questions.

Quand on aborde la mécanique quantique et la dualité onde-corpuscule, on est amené à considérer deux visions : La physique Newtonienne et la physique ondulatoire.

D'après Newton et la mécanique classique, une particule de masse m est, à un instant t, dotée d'un état avec r sa position dans l'espace et p son impulsion réelle (quantité de mouvement je présume). Donc quand on observe une particule à un moment donné, elle se trouve à un endroit précis et dispose d'un mouvement précis, dicté par son inertie et les forces qui s'exercent sur elle, je me trompe ?

D'après Shrödinger, une particule dispose d'une fonction d'onde probabiliste qui donne à une particule sa probabilité d'être à un endroit de l'espace(-temps ?) à un instant donné.
J'ai fait une petite recherche sur le net, et on me dit que , avec Psi fonction continue de l'espace-temps.
Donc si je somme toutes les probabilités de présence d'une particule dans l'espace et le temps, j'obtiens 1, normal. Mais je vois pas d'où vient , ni ce que veut dire explicitement cette formule.



Il est dit que la frontière entre méca classique et méca quantique est atteinte lorsque l'on est amené à "comparer le de la particule à la longueur caractéristique du phénomène".
Gros moment de bug.
Qu'est-ce que veut dire cette phrase ?

[Skullkid]

Salut

Bonjour, j'ai deux questions.

Quand on aborde la mécanique quantique et la dualité onde-corpuscule, on est amené à considérer deux visions : La physique Newtonienne et la physique ondulatoire.

D'après Newton et la mécanique classique, une particule de masse m est, à un instant t, dotée d'un état avec r sa position dans l'espace et p son impulsion réelle (quantité de mouvement je présume). Donc quand on observe une particule à un moment donné, elle se trouve à un endroit précis et dispose d'un mouvement précis, dicté par son inertie et les forces qui s'exercent sur elle, je me trompe ?

C'est exact. Pour ce qui est de la mécanique quantique, en fait les fonctions d'ondes en elles-mêmes n'ont pas d'interprétation physique, ce à quoi on peut donner un sens c'est leur module au carré, qui est une densité de probabilité. C'est-à-dire que est la probabilité de trouver ta particule dans le volume infinitésimal autour de la position 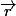, tu peux voir ça comme une définition des fonctions d'onde. En coordonnées cartésiennes, le c'est un dxdydz donc la probabilité en question c'est celle que ta particule soit dans [x,x+dx]*[y,y+dy]*[z,z+dz].

Détail important : il n'y a pas d'espace-temps en mécanique quantique, l'espace-temps est un concept relativiste et la relativité ne s'entend pas trop bien avec la mécanique quantique... Comme en mécanique classique, le temps n'est ici qu'un paramètre.

L'idée c'est qu'en réalité, une particule ça n'a pas de position bien définie, uniquement une probabilité de présence. Mais cette probabilité va être négligeable (typiquement elle décroît spatialement exponentiellement) en dehors d'un volume de l'ordre de où est la longueur caractéristique de décroissance de l'exponentielle (qui va être du même ordre de grandeur que la longueur d'onde de la particule). Donc si tu t'intéresses à un phénomène dont la longueur caractéristique est grande devant , l'espace dans lequel la probabilité de présence de ta particule est non négligeable va ressembler à un point et donc tout se passe comme si la particule avait une position et tu peux faire de la mécanique classique (c'est d'ailleurs un exercice intéressant de retrouver le PFD newtonien à partir des postulats de la mécanique quantique). Mais si ton phénomène se produit à des échelles de l'ordre de (ou plus petites que) , il faut prendre en compte le fait que ta particule se propage, qu'elle est "un peu partout à la fois", et passer par les fonctions d'onde.

[Anonyme]

@Skullkid

Est ce que cela explique : l'expérience du chat de Schrodinger ?

Et d'après ce que j'ai entendu récemment :
c'est , à ce jour , une "application physique" (en France et au USA via 2 techniques différentes)
qui soit disant va générer beaucoup d'innovations techniques d'ici une quinzaine d'années ?

[Kikoo <3 Bieber]

Skullkid : Merci pour cette super réponse ! Je la lis et j'essaierai de m'en imprégner.

Ptitnoir : en ce qui concerne le paradoxe de Shrödinger, j'ai lu que cela se base sur la superposition d'états quantiques. Skullkid, Math ou d'autres connaisseurs t'en diront d'avantage ;)
Mon prof de l'année dernière avait fait sa thèse sur une application de la mécanique quantique en informatique. Il me semble que c'est à propos de cette superposition d'états, qui pourrait augmenter la vitesse de traitement des ordinateurs, en faisant passer celle-ci d'un niveau exponentiel à d'avantage, ou de polynomial à exponentiel, je me rappelle plus trop.
Faudrait que je repasse au lycée pour lui demander ^^

[Skullkid]

Schrödinger a imaginé son expérience du chat pour mettre en lumière le caractère hautement non intuitif de la mécanique quantique et en particulier d'une de ses interprétations (celle dite de Copenhague).

Un physicien, par défaut, c'est câblé pour essayer de donner une interprétation physique à tous les énoncés mathématiques qu'il utilise. Le problème avec la mécanique quantique c'est qu'il y a beaucoup de phénomènes qui refusent de se laisser interpréter de façon satisfaisante autrement que mathématiquement. Le plus célèbre de ces phénomènes est celui des états superposés. L'exemple du chat "à la fois mort et vivant" est une extrapolation de ce phénomène à un objet macroscopique, non quantique. Pour mettre précisément le doigt sur le détail qui fâche, il faudrait faire un peu de maths mais il est tard...

Pour simplifier, la mécanique quantique dit que parmi les états possibles d'un système physique, il y en a qui sont plus physiques que les autres, dans le sens où ils sont observables alors que d'autres ne le sont pas. Mais rien n'interdit aux systèmes physiques d'être dans un état non observable tant qu'on ne l'observe pas, et de fait, certains phénomènes observés expérimentalement ne se justifient à l'heure actuelle que si on admet l'existence de ces états non observables. L'interprétation de Copenhague ça consiste en gros à dire qu'être dans un état non observable ça peut, au mieux, s'interpréter comme être à la fois dans plusieurs états observables distincts (donc exclusifs les uns des autres), et que de toute façon ça n'a pas de sens d'essayer de comprendre la nature d'état inobservable puisque personne n'en a jamais observé.

Cette vision des choses est frustrante puisqu'elle consiste à dire que "ça marche mais on ne sait pas pourquoi", ou plutôt "ça marche mais on ne sait pas ce que c'est". Il y a d'autres interprétations possibles, bien que celle de Copenhague reste la plus courante, mais ça reste des interprétations, chacune avec leur lot de bizarreries conceptuelles. Après, c'est une question de goût et de convictions.

En revanche je n'ai pas compris ta phrase sur "l'application physique" d'ici une quinzaine d'années. De quelle application parles-tu ? Sans doute les ordinateurs quantiques, comme le suggère Kikoo <3 Bieber, et qui seraient en effet une sacrée révolution (une quinzaine d'années ça me semble un peu optimiste, mais sait-on jamais), mais la mécanique quantique a déjà beaucoup d'applications à l'heure actuelle...

[Anonyme]

@Skullkid

Au niveau des applications , je me souviens que l'article "parle" en effet d'informatique.

C'est quand même des trucs de ouf : une équipe de 10 chercheurs qui travaille pendant 10 ans sur une théorie qui date de plus de 70 balais
et qui essaient et qui réussissent à construire des miroirs dit "parfaits" !

On est effectivement dans un autre monde : le monde de la RECHERCHE