HOLA tt le monde !
je suis au terminale SM (apartir du début du prochain an scolaire ) mais je voulais un peu m'exercer , alors j'ai commencé par le chapitre de la dynamique , j'ai compris la 1ère leçon(la cinematique) mais j'ai trouvé du mal à résoudre ce probleme :briques: c'est un peu complexe :briques: ...
( à un point o d'un repère (oxy) on lance un corps de masse M qu'on peut considérer ponctuel , et cela avec une vitesse V* dont le vecteur forme un angle A avec l'axe (oy) , et tout cela à partir d'un instant t=0....alors la trajectoire est sous forme de parabole....donc ce qui est demandé c'est de déterminer l'expression de l'accelération tangentielle (at ) à un point M (appartenant à la parabole) lorsque le corps arrive à ce point à un instant t'. et cela en fonction de : v* , g , A (l'angle avec (oy)) et t' :briques: ))
je sais que ça peut etre résolu à l'aide du repère FREINET au point M mais je sais pas comment :triste:
merci d'avance pour vous tous
L'accelération tangentielle
12 messages
- Page 1 sur 1
Salut,
Fais d'abord un dessin.
Notons (Ox) l'horizontale et (Oz) la verticale dirigé vers le haut et (Oy) la troisième composante.
PS : j'ai changé les axes, je trouvais ça mieux mais tu pourras les rechanger.
On a donc)
Or,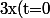=y(t=0)=z(t=0)=0) car
car 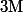 est en
est en 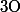 .
.
De plus, sur le schema, tu vois facilement que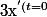=v_ocos(\alpha)) ,
, =0) et
et 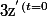=v_o sin(\alpha)})
On a donc par application de la relation fondamentale de la dynamique :
***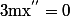 et donc
et donc )
Finalement,=v_ocos(\alpha)t+x_o)
Or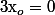 d'après le repère donc
d'après le repère donc =v_ocos(\alpha)t})
***On a également=0}) pour tout
pour tout 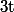
***Enfin, on a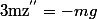 soit
soit 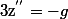 donc
donc )
Donc=\frac{-1}{2}gt^2+v_osin(\alpha)t})
En éliminant le temps dans l'une des équations, tu obtients la trajectoire du mobile :
=\frac{-gx^2}{2v_0^{2}cos^2(\alpha)}+xtan(\alpha)}) (on te demander de montrer que c'est une parabole)
(on te demander de montrer que c'est une parabole)
Il suffit ensuite de dériver deux fois pour trouver l'accélération tangentielle non ?
PS : ya longtemps que je n'ai pas fait de physique...c'est quoi exctement l'accélération tangentielle ?
Thomas G :zen:
Fais d'abord un dessin.
Notons (Ox) l'horizontale et (Oz) la verticale dirigé vers le haut et (Oy) la troisième composante.
PS : j'ai changé les axes, je trouvais ça mieux mais tu pourras les rechanger.
On a donc
Or,
De plus, sur le schema, tu vois facilement que
On a donc par application de la relation fondamentale de la dynamique :
***
Finalement,
Or
***On a également
***Enfin, on a
Donc
En éliminant le temps dans l'une des équations, tu obtients la trajectoire du mobile :
Il suffit ensuite de dériver deux fois pour trouver l'accélération tangentielle non ?
PS : ya longtemps que je n'ai pas fait de physique...c'est quoi exctement l'accélération tangentielle ?
Thomas G :zen:
:triste: je crois là que tu parle de l'accelération angulaire (teta) mais la relation de
l'accelération tangentielle c'est a=la racine carré de (at)²+(an)² tel que :
at=accelération tangentielle et an=accelération normale dans le repère de freinet
:triste: et en plus de tout ça le point M n'est pas identique à O c'est un point appartenant à la parabole, car si tu retourne à l'énoncé tu remarque que le corps arrive à ce point à un autre instant t' différent de t=o (donc impossible que les deux points sont identique puisque le corps est en mouvement :!: )
mais pour le shema je sais pas comment faire pour le poster , t'sais comme tu peux le remarquer (membre naturel) :girl2:........ donc mnt je crois que j'ai deux problèmes à résoudre d'abord comment poster un shema et le 2ème c'est mon exo :briques:
l'accelération tangentielle c'est a=la racine carré de (at)²+(an)² tel que :
at=accelération tangentielle et an=accelération normale dans le repère de freinet
:triste: et en plus de tout ça le point M n'est pas identique à O c'est un point appartenant à la parabole, car si tu retourne à l'énoncé tu remarque que le corps arrive à ce point à un autre instant t' différent de t=o (donc impossible que les deux points sont identique puisque le corps est en mouvement :!: )
mais pour le shema je sais pas comment faire pour le poster , t'sais comme tu peux le remarquer (membre naturel) :girl2:........ donc mnt je crois que j'ai deux problèmes à résoudre d'abord comment poster un shema et le 2ème c'est mon exo :briques:
nada-top a écrit:donc mnt je crois que j'ai deux problèmes à résoudre d'abord comment poster un shema et le 2ème c'est mon exo :briques:
En ce qui concerne le premier problème, d'abord tu crées une image (avec Paint, en scannant un dessin à la main, avec un programme, avec un utilitaire quelconque... là je ne peux pas t'aider),
ensuite tu vas sur le site http://www.imageshack.us/ par exemple (il y a en a plusieurs, je n'en connais qu'un), et tu donnes ton image au site, qui te renvoies des liens que tu n'auras plus qu'à insérer dans ton post sur le forum.
Pas dur ! Faut quand même créer l'image d'abord !
@+
nada-top a écrit:Hé les amis ,,, ça donne toujours rien :help:
Bon ! Tu peux calculer le vecteur vitesse
Alors
c'est clair ça mais le probloeme comment déterminer d'abord le vecteur OM (désolé je maitrise pas le latex) on connait meme pas l'angle qu'il forme avec les axes du repère ... car il faut démontrer ça pour tout point appartenant au parabole sauf O 
on sait juste qu'on a lancé le corps du point O PAR une vitesse V0 dont le vecteur forme un angle (teta) avec (oz) .... voir schema

on sait juste qu'on a lancé le corps du point O PAR une vitesse V0 dont le vecteur forme un angle (teta) avec (oz) .... voir schema
nada-top a écrit:c'est clair ça mais le probloeme comment déterminer d'abord le vecteur OM (désolé je maitrise pas le latex) on connait meme pas l'angle qu'il forme avec les axes du repère ... car il faut démontrer ça pour tout point appartenant au parabole sauf O
on sait juste qu'on a lancé le corps du point O PAR une vitesse V0 dont le vecteur forme un angle (teta) avec (oz) .... voir schema
Bien sûr, mais je croyais que les explications de Nekros t'avaient suffi ! Bon, il ne t'a pas vraiment facilité la tâche car il a changé les axes, et, semble-t-il la signification de l'angle A... Mais l'idée est là !
En reprenant ton schéma, on connaît
Comme la force appliquée est uniquement le poids, la RFD disant
On en déduit,
Et tu connais exactement les équations du mouvement, les composantes du vecteur vitesse à tout instant
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :


