L'accéleration tangentielle encore!!
De la mécanique au nucléaire, nos physiciens sont à l'écoute
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 13 Aoû 2006, 21:05
par nada-top » 13 Aoû 2006, 21:05
[FONT=Palatino Linotype]
Salut,je reviens sur cet exo [/FONT]
http://www.maths-forum.com/showthread.php?t=16991&page=2&pp=10&highlight=acc%E9l%E9ration+tangentielle[FONT=Palatino Linotype]j'ai repéré une faute dans mon résumé(grace à votre aide bien sur) mais j'en suis pas sure , je dois conclure plutot : [/FONT]
^2 + 1 } \right ))
[FONT=Palatino Linotype]si oui quand est-ce que[/FONT]
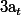
[FONT=Palatino Linotype]peut etre négative et quelle est l'interprétation graphique dans ce cas ?[/FONT]
[FONT=Palatino Linotype]
Merci d'avance pour vos réponses[/FONT]
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 13 Aoû 2006, 23:40
par nada-top » 13 Aoû 2006, 23:40
[FONT=Palatino Linotype]alors ça donne quoi???[/FONT] :crash:
[FONT=Palatino Linotype]je vous attend [/FONT]
-
flaja
- Membre Rationnel
- Messages: 904
- Enregistré le: 02 Juil 2006, 16:24
-
 par flaja » 14 Aoû 2006, 19:36
par flaja » 14 Aoû 2006, 19:36
Bonjour nada-top
accélération :

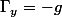
vitesse :

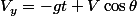
accélération tangentielle :
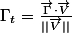

-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 14 Aoû 2006, 21:46
par nada-top » 14 Aoû 2006, 21:46
[FONT=Palatino Linotype]salut flaja,[/FONT][FONT=Palatino Linotype]peut etre que tu n'as pas lancé un coup d'oeil sur l'autre page , je suis tout à fait d'accord avec toi jusqu'à ce point [/FONT] 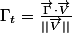 [FONT=Palatino Linotype], d'ailleurs j'ai aboutit à la meme chose....mais pour la conclusion je crois pas .
[FONT=Palatino Linotype], d'ailleurs j'ai aboutit à la meme chose....mais pour la conclusion je crois pas .
pour [/FONT] 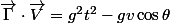 [FONT=Palatino Linotype](c juste ça)
[FONT=Palatino Linotype](c juste ça)
mais[/FONT]
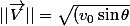^2 + (-gt+V_0 \cos\theta)^2})
[FONT=Palatino Linotype]
d'abord il y a confusion entre [/FONT]
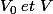
[FONT=Palatino Linotype]
concernant[/FONT]
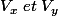
[FONT=Palatino Linotype]
et d'autre part je crois que tu n'as calculé que [/FONT] ^2})
[FONT=Palatino Linotype]
pour la norme de[/FONT]
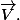
[FONT=Palatino Linotype]
cependant la question était d'exprimer [/FONT]
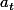
[FONT=Palatino Linotype]
seulement en fonction de [/FONT]

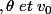
(sans t) [FONT=Palatino Linotype]
c'est pour cela que j'ai simplifié la 1ère expression de[/FONT]
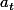 [FONT=Palatino Linotype]et j'ai obtenu la valeur absolue [/FONT] ..
[FONT=Palatino Linotype]et j'ai obtenu la valeur absolue [/FONT] ..[FONT=Palatino Linotype]
alors pour étre plus claire voilà ce que j'ai fait : [/FONT] .(-gt+V_0\cos\theta)}{sqrt{(V_0\sin\theta)^2+(-gt+V_0\cos\theta)^2}}\;)
^2 = \frac{g^2.(-gt+V_0\cos\theta)^2}{(-gt+V_0\cos\theta)^2\left(\left ( \frac{V_0\sin\theta}{-gt+V_0 cos\theta} \right )^2+1\right)}\;)
^2 = \frac{g^2}{\left ( \frac{V_0\sin\theta}{-gt+V_0cos\theta} \right )^2+1})
d'ou le résultat :
^2 + 1 } \right ))
(c'est pour cela que je parlais de la valeur absolue.
[FONT=Palatino Linotype]merci en tous cas flaja j'espère que t'as compris ma question maintenant : quelle est l'interprétation graphique lorsque [/FONT]
) [FONT=Palatino Linotype]est négative?[/FONT]
[FONT=Palatino Linotype]est négative?[/FONT] :++:
@+
-
flaja
- Membre Rationnel
- Messages: 904
- Enregistré le: 02 Juil 2006, 16:24
-
 par flaja » 15 Aoû 2006, 09:52
par flaja » 15 Aoû 2006, 09:52
Bonjour nada-top
nos formules sont identiques (au signe près) :
ce que j'appelle V est la vitesse initiale
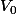
(ambigüité de l'énoncé)
Remarquant que
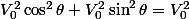
, tu obtiendras ma formule.
L'accélération tangentielle n'est pas constante. Il faut donc indiquer le point où on la calcule soit par son temps, soit par sa position.
Ici tu sembles avoir choisi le temps (facteur
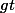
)
Comme je n'ai pas perdu le signe en élevant au carré
le signe de
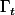
est celui de
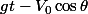
...
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 15 Aoû 2006, 10:33
par nada-top » 15 Aoû 2006, 10:33
Arf j'ai fais une jolie erreur :hum: ...il s'agit bel et bien de trouver l'expression en fonction de

,
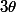
,

et
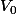
...d'ailleurs il se peut pas que
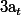
soit indépendante du temps et en + le

exsiste toujours dans mon expression et je l'ai pas choisi j'ai juste simplifié l'expression .
pour ce qui est de

et
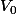
j'ai dit qu'il y a confusion car tu as choisi le meme

pour
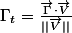
que pour l'expression de
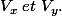
.
pourtant pour ta formule oui c'est identique à la mienne.
mais la question est toujours posée: (l'interprétation graphique pour
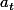
(-) )
@+
-
flaja
- Membre Rationnel
- Messages: 904
- Enregistré le: 02 Juil 2006, 16:24
-
 par flaja » 15 Aoû 2006, 11:01
par flaja » 15 Aoû 2006, 11:01
signe de
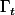
: le même que celui de
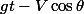
négatif (freinage) tant que
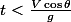
positif (accélération) ensuite
Remarque :
apogée :

, soit :
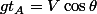
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 15 Aoû 2006, 11:19
par nada-top » 15 Aoû 2006, 11:19
donc peut-on dire qu'avant l'apogée
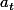
est négative et aprés elle est positive :hein:
-
flaja
- Membre Rationnel
- Messages: 904
- Enregistré le: 02 Juil 2006, 16:24
-
 par flaja » 15 Aoû 2006, 12:59
par flaja » 15 Aoû 2006, 12:59
Bien sûr.
L'accélération étant toujours vers le bas, quand la vitesse est orientée vers le haut l'accélération tangentielle est négative et inversement.

l'accélération tangentielle est du signe opposé à la composante y de la vitesse.
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 15 Aoû 2006, 13:16
par nada-top » 15 Aoû 2006, 13:16
ok merci beaucoup flaja :we: c'est claire
maintenant je réfléchis à autre chose:l'expression de

(le rayon de la courbure) mais je vais d'abord faire mes calculs et si je trouve toujours des problemes je te ferais signe. je connais déjà la relation
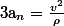
@+
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 21 Aoû 2006, 22:57
par nada-top » 21 Aoû 2006, 22:57
bonsoir,
ah vraiment horribles les calculs de ce petit
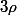
:hum: , quelqu'un aura de la patience pour me simplifier l'expression de
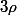
...je sèche complétement quand il s'agit de ce genre de calculs , ou plutôt y a pas une expression générale ??
xie xie :lol3:
-
flaja
- Membre Rationnel
- Messages: 904
- Enregistré le: 02 Juil 2006, 16:24
-
 par flaja » 25 Aoû 2006, 20:06
par flaja » 25 Aoû 2006, 20:06
Quand on prend des problèmes au hazard ils n'ont aucune raisons de se simplifier.
C'est pourquoi on se contente de résoudre les problèmes réels numériquement.
Expression générale du rayon de courbure :
rappel :
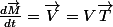
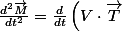=\frac{dV}{dt}\vec T + V \frac{d\vec T}{dt} = \Gamma_t\vec T + V \frac{d\vec T}{ds}\frac{ds}{dt})
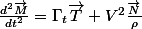
Pour obtenir
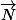
et

, il faut faire :

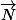
étant choisi unitaire :
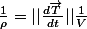
Je crois.
-
patrick
- Messages: 3
- Enregistré le: 26 Aoû 2006, 15:45
-
 par patrick » 26 Aoû 2006, 16:49
par patrick » 26 Aoû 2006, 16:49
salut ,si t'as une acceleration tangentielle negative alors puisque cette acceleration tangentielle est la derivee de la composante tangentielle de la vitesse je deduis que la composante tangentielle decroit donc le mouvement est freine et une composante de la force de freinage est dirigee suivant la tangente a la trajectoire c'est tout ce que l'on peut conclure sur ce pb arete
de te :mur:
-
flaja
- Membre Rationnel
- Messages: 904
- Enregistré le: 02 Juil 2006, 16:24
-
 par flaja » 27 Aoû 2006, 11:07
par flaja » 27 Aoû 2006, 11:07
En partant de :
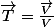
en remarquant que
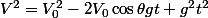
d'où :
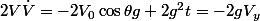
(
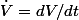
)

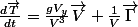
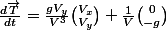



d'où
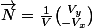
(unitaire)
et
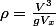
remarque :
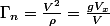
et
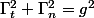
J'espère que c'est enfin terminé !
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 27 Aoû 2006, 11:26
par nada-top » 27 Aoû 2006, 11:26
Re,
je me demande vraiment pourquoi tt ça , on a
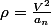
et on a

. on a déjà trouvé l'expression de
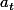
donc il suffit de substituer , peut etre vous n'avez pas compris mon probleme je cherche à exprimer

en fonction de
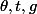
et
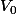
mais j'arrive pas à simplifier l'expression .
[FONT=Palatino Linotype]Merci[/FONT]
-
flaja
- Membre Rationnel
- Messages: 904
- Enregistré le: 02 Juil 2006, 16:24
-
 par flaja » 27 Aoû 2006, 13:04
par flaja » 27 Aoû 2006, 13:04
Tous ce développement pour éviter l'indétermination sur le signe de
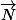
.
avec
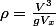
le problème est terminé.
il suffit de remplacer
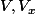
par leurs valeurs déjà connues :
^3}{gV_0\sin\theta})
Et il n'y a rien qui se simplifie davantage.
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 27 Aoû 2006, 17:40
par nada-top » 27 Aoû 2006, 17:40
ah oui j'ai pigé ..merci beaucoup :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
