Vrai / faux sur les limites de fonction

[MARJORIE 35390]

Bonjour;
alors voilà j'ai une affirmation à laquelle je dois dire si elle est vraie ou fausse, pour moi elle est vraie mais je voudrais votre avis .
C'est : " si lim quand x tend vers + infini f(x)/g(x)=1 alors lim quand x tend vers + infini f(x)-g(x) =0 "
Vrai ou faux ?

[soradia1]

Je crois bien que c'est vrai, si tu divise l'expression f(x) - g(x) par g(x), tu auras zéro.

Seulement je trouve que c'est trop facile pour être ça!!

[keofran]

Diviser par g(x) c'est évalué la limite d'une autre fonction et ça ne répond donc pas à la question.
Pour utiliser la limite vers 1, il faudrait factoriser par g(x), mais on ne pourra pas conclure, vu qu'on ne connaît pas la limite de g.

Essayons plutôt le contre-exemple, avec par exemple les polynômes.

Qu'est-ce que ça peut donner ?

[MARJORIE 35390]

Je ne comprends pas ce que vous voulez dire avec les polynomes ? :/

[MARJORIE 35390]

Je crois bien que c'est vrai, si tu divise l'expression f(x) - g(x) par g(x), tu auras zéro.

Seulement je trouve que c'est trop facile pour être ça!!

Oui ça me parait trop facile aussi c'est pour ça c'est bizarre !

[chombier]

Je ne comprends pas ce que vous voulez dire avec les polynomes ? :/

Cherches deux polynômes P et Q tel que lim P/Q = 0 et lim P-Q différent de 0

[MARJORIE 35390]

Cherches deux polynômes P et Q tel que lim P/Q = 0 et lim P-Q différent de 0

je dois plutot chercher des polynomes P et Q tel que P/Q soit égal à 1 ?

[MARJORIE 35390]

je dois plutot chercher des polynomes P et Q tel que P/Q soit égal à 1 ?

mais c'est impossible de trouver des polynomes pour que P/Q=1 et P-Q différent de 0 ? :/

[chombier]

mais c'est impossible de trouver des polynomes pour que P/Q=1 et P-Q différent de 0 ? :/

Cherches encore C'est possible.

Rappelles toi, si ça peux t'aider, que la limite d'une fraction rationnelle P/Q à l'infini est égale à la limite du quotient des monômes de plus haut degré.

[MARJORIE 35390]

Cherches encore C'est possible.

Rappelles toi, si ça peux t'aider, que la limite d'une fraction rationnelle P/Q à l'infini est égale à la limite du quotient des monômes de plus haut degré.

Faut-il que chaque polynome P et Q soient égaux?

[keofran]

Soyons plus précis et n'oublie pas de chercher sincèrement, avec au besoin ton cours sous les yeux. Si tu veux progresser il faut être actif.

Un polynôme est une somme de comme ou .

Le premier polynôme est de degré 1, parce que l'exposant du le plus élevé est 1. Ce type de polynôme de degré 1 donne les fonctions affines du type .

Et c'est justemet ce qu'on va chercher, 2 fonctions affines et telles que et

[MARJORIE 35390]

Soyons plus précis et n'oublie pas de chercher sincèrement, avec au besoin ton cours sous les yeux. Si tu veux progresser il faut être actif.

Un polynôme est une somme de comme ou .

Le premier polynôme est de degré 1, parce que l'exposant du le plus élevé est 1. Ce type de polynôme de degré 1 donne les fonctions affines du type .

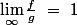
Et c'est justemet ce qu'on va chercher, 2 fonctions affines et telles que et

f(x) doit donc être de la forme: ax+b et g(x) doit être de la forme: ax^2+bx+c?

[keofran]

Non, relis bien, j'ai dit 2 fonctions affines. Cherche des fonctions simples et forcément différentes sinon elles vérifieront l'affirmation de l'énoncé.

[MARJORIE 35390]

f(x) doit donc être de la forme: ax+b et g(x) doit être de la forme: ax^2+bx+c?

si on prend : f(x) = x^2+2 et g(x)= x^2 +2 on trouve f(x)/g(x)=1 mais f(x)-g(x)=0 :/

[MARJORIE 35390]

si on prend : f(x) = x^2+2 et g(x)= x^2 +2 on trouve f(x)/g(x)=1 mais f(x)-g(x)=0 :/

si f(x)=x+5 et g(x) = 2x+10, est ce que ça peut le faire ?

[keofran]

A toi de nous le dire.

[MARJORIE 35390]

A toi de nous le dire.

non ça marche pas , je pense avoir trouver:
si f(x)= 2x+4 et g(x)=2x+7 , lim de f(x)/g(x)=1 et lim f(x)-g(x) différent de 0 c'est ça ?

[keofran]

Oui :we:

Et on peut faire encore plus simple, mais ta solution est suffisante.

[MARJORIE 35390]

Oui :we:

Et on peut faire encore plus simple, mais ta solution est suffisante.

Merci beaucoup pour votre aide précieuse, je suis enfin débloquée .