une idée pour calculer cette limite :
merci :we:
Une limite
7 messages
- Page 1 sur 1
par johnjohnjohn » 02 Jan 2007, 17:03
sue a écrit:salut !
une idée pour calculer cette limite :
merci :we:
A condition de connaitre la dérivée de la fonction arctan, j'ai bien pensé dire que
en posant g / :
Ton expression peut aussi s'écrire :
En déterminant séparement
et
On lève peut être l'indétermination.
Je crains néanmoins d'avoir écris d'énormes bêtises ....
par allomomo » 02 Jan 2007, 17:10
Salut,
=\frac{1}{1+x^2})
Idée de démonstration :
tan(arctan(x))=x .... (une composée)
Idée de démonstration :
tan(arctan(x))=x .... (une composée)
par sue » 02 Jan 2007, 17:19
oui je connais la dérivée de arctan(u) et je cherche justement si g (que vous avez posé John ) est biien dérivable en 
.
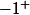
c'était ça en fait la quetion posé dan mon exo .
ça peut parataire une question un peu bete , mais est-ce qu'on a le droit de calculer g'(-1+) quand on nous demande d'étudier la dérivabillité ?
c'était ça en fait la quetion posé dan mon exo .
ça peut parataire une question un peu bete , mais est-ce qu'on a le droit de calculer g'(-1+) quand on nous demande d'étudier la dérivabillité ?
par sue » 02 Jan 2007, 17:31
Re -
oui et alors ? ça prouve qu'il y a une FI .
Et le tout diverge vers
pkoi ?
par sue » 02 Jan 2007, 18:05
ok ok je l'ai eu .
on a : - g(-1)}{x+1} =\lim_{x\to -1^+} \frac{arctan(u(x)) - \frac{\pi}{4}}{u(x)-u(-1)} \times \frac{u(x) - u(-1)}{x+1} = \lim_{x\to -1^+} \frac{u(x)) - u(-1)}{x+1}\times \lim_{t\to1} \frac{arctan(t) - arctan(1)}{t-1} =...)
la 1ère limite diverge vers
et la 2ème est arctan'(1)=1/2
donc le tt diverge vers
merci à vous
on a :
la 1ère limite diverge vers
donc le tt diverge vers
merci à vous
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 90 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :