Trouver l'équation d'une parabole

[Anonyme]

Bonjour , j'ai une parabole à laquelle appartient le point A(3;1) , en ce point A il y a une tangente de 60° , l'axe de symétrie de la parabole est x = -1 , trouver son équation .

Moi je ferai comme çà :

l'équation d'une parabole c'est y = ax²+bx+c , donc sa dérivée c'est : y' = 2ax + b

on peut donc écrire : 1 = 2*tan60° + b , b = -2.46

pour a je fais :

1 = 2*3*a - 2.46 , a = 0.58

je suis sur la bonne voie?

[zyfux]

Salut!
Déjà c'est une bonne idée d'avoir posé y=ax^2+bx+c (désolé je sais pas faire les carrés :confused: :)
Après tu sais que l'axe de symétrie est en -1 donc tu peux en deduire la position du sommet de la parabole.
Bonne idée pour la tangente! Par contre je ne suis pas sur que cela puisse s'exprimer par tan60 :confused:
Sinon il me semble que t'es sur la bonne voie. Si tu trouve bien le sommet en x=-1 ça devrait être bon!

[Anonyme]

le problème c'est que si tu prends les valeurs que j'ai trouvé pour a et b , ben -b/2a ne donne pas -1 ...

[leibniz]

Salut,
Organisons les données:
A(3,1) appartient à la parabole => 9a+3b+c=1 (1)
En ce point A il y a une tangente de 60° => tang60°=6a+b (2)
l'axe de symétrie de la parabole est x = -1 => A'(-5,1) appartient a la parabole.( A' est la symeterie du point A par rapport a l'axe x=-1) => 25a-5b+c=1 (3)
Tu n'as qu'a resoudre le systeme composé des equations (1), (2) est (3)
N.B: Eviter de donner des valeurs approchées.
Par exemple tan(60°) =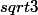 (éviter d'ecrire 1.73 )
Bonne chance.

[Anonyme]

donc la méthode sur laquelle j'étais parti était totalement fausse :( , ya jsute un petit soucis : pour ta 2ème équation , tan60° = 6a + b , je comprends fort bien que tu as fait dans ta tête 2ax +b = y' , en prenant l'abscisse 3 j'ai bien 6a + b , mais le y' , pourquoi le remplacer par tan60° et pas par la valeur de y , parce que y' signifie le coefficient directeur?

[leibniz]

Oui tu as tout à fait raison, y' représente le coefficient directeur de la tangente et il représente aussi le tangente de l'angle entre la tangente de la courbe et l'axe des abscisse ( 60° dans ce cas). Tu peux jeter un coup d'oeuil sur ton cours, peut-etre tu vas trouver la demonstration de ce que j'ai dit.
Bonne courage :)

[Anonyme]

j'essaye de résoudre ton système :

9a+3b+c=1
tang60°=6a+b
25a-5b+c=1

b = - 6a

0 = -16a + 8b
0= -16a + 8 - 48a
0 = 64a + 8
a = -/8

b = - (6*-) / 8
b = 7/4 *

1 = (-9) / 8 + (21) / 4 + c
1 = 33/8
c = 1 - 33/8 = (8 - 33)/8

voilà j'ai trouvé les valeurs de a , b , et c , elles me paraissent bien compliquées

[leibniz]

Oui, et cela est du au valeurs choisies.
Bien sur t'as pas fait de fautes en calculant.
Allez Bonne continuation :)

[Anonyme]

ça veut dire que ce sont les bonnes valeurs ? , mais c'est pas possible , car a devrait être positif

[rene38]

Bonjour

Erreur de calcul ici :
0= -16a + 8 - 48a
0 = -64a + 8

on trouve finalement :