Bonjour,je suis en première S, et j'ai un problème avec un DM de maths.
Voici l'énoncé de mon DM, je vous dirais ensuite où je bloque.
(je ne sais pas comment on écrit alpha et bêta donc je l'écrirai: (a) pour alpha et (b) pour bêta, (g) pour gamma)
Préliminaire:
On considère l'équation (E): (a)x²+(b)x+(g) =0, où (a), (b) et (g) sont des réels, (a) est non nul.Démontrer que si (E) a 2 solutions distinctes X1 et X2, alors X1+X2= -(b)/(a) et X1*X2=(g)/(a).
Ca je l'ai démontré
Le plan est muni d'un repère orthonormé. On désigne par (P) la parabole d'équation y= (1/4)x² et par A le point de coordonnées (a; b) où a et b sont 2 réels quelconques. On dira qu'une droite non parallèle à l'axe des ordonnées est tangente a (P) lorsqu'elle coupe la parabole qu'ne un seul point.
1. Construire (P) avec le plus de précisions possible.Ca je l'ai fait
2. On désigne par Dm la droite passant par A de coefficient directeur m, m étant un réel quelconque. Déterminer une équation de Dm.
J'ai trouvé Dm: y = mx+b-am
3.A quelle condition sur a et b, existe-t-il une droite Dm tangente à la parabole? Donner une interprétation graphique du résultat. C'est ici que je bloque.Je trouve ce système:
{y= mx+b-am
y=(1/4)x²
et ensuite je bloque
Je vous donne la suite de l'énoncé:
4. Losquil existe deux droites distinctes Dm qui sont tangentes à la parabole, où doit se trouver le point A pour que les droites soient perpendiculaires ?
5. vérifier la propriété précédente lorsque les coordonnées de A sont (1,5 ;-1). Donner dans ce cas des équations des droites Dm, tracer ces droites.
6. dans cette question, on suppose que le point A est tel quil existe deus droites perpendiculaires D1 et D2 passant par A et tangentes à la parabole.On nomme T1 le point commun à la parabole et à D1, T2 le point commun à la parabole et à D2, et I le milieu de [T1T2]. Démontrer que la droite (AI)est parallèle à laxe des ordonnées et que le milieu de [AI] est sur la parabole.
Voilà. Je n'ai pas essayer la 4,5 et 6 vu que je suis bloqué a la 3...
Merci beaucoup d'avance de m'aider (et me dire peut etre si j'ai faux a la 2??)
Trinôme du 2nd Degré, Parabole, Plan (urgent)
13 messages
- Page 1 sur 1
merci mais...
Alors merci pour ton aide, mais je ne vois pas comment faire après!! :S
Juste une autre étape s'il te plait?? Merci beaucoup d'avance!
Il faut peut être faire avec l'identité remarquable a²-b²??
Juste une autre étape s'il te plait?? Merci beaucoup d'avance!
Il faut peut être faire avec l'identité remarquable a²-b²??
Bonjour encore! :ptdr:
As-tu vu ce qu'est le discriminant ?:hein:
?:hein:
Puisqu'en fait dans mon DM on a étudié le signe de 4(mx+b-am)-x^2 afin de trouver les racines éventuelles et savori pour quelels valeurs çà s'annule.Mais je dois t'avouer que nous avions les coordonnées de A.Ce n'atait a et b mais 2 et 0.Donc c'était forcément plus facile.En tout cas la démarche était la même,et pour n'importe quel exo on faisait cette démarche.
Mais as-tu vu le discrimnant?pcq si non il faut peut-être adopter une toute autre démarche... :hum:
Comme l'as précisé s@m,ce genre de DM nous a fait bcp baver en 1èreS...
As-tu vu ce qu'est le discriminant
Puisqu'en fait dans mon DM on a étudié le signe de 4(mx+b-am)-x^2 afin de trouver les racines éventuelles et savori pour quelels valeurs çà s'annule.Mais je dois t'avouer que nous avions les coordonnées de A.Ce n'atait a et b mais 2 et 0.Donc c'était forcément plus facile.En tout cas la démarche était la même,et pour n'importe quel exo on faisait cette démarche.
Mais as-tu vu le discrimnant?pcq si non il faut peut-être adopter une toute autre démarche... :hum:
Comme l'as précisé s@m,ce genre de DM nous a fait bcp baver en 1èreS...
Oui,soit tu essaie de facoriser -x^2) ,afin que tes racines apparaissent plus nettement.
,afin que tes racines apparaissent plus nettement.
Le but en fait est de voir le signe du discriminant en fonction de m.
Selon la valeur de ton discriminant,tu auras plus ou moins de racines réelels,donc plus ou moins d'intersections...
Si tu veux l'ami je te donner la correction de notre exercice afin que tu t'en inspires (car c'est la même chose sauf que toi c'est plus général étant donné que tu n'as pas les coordonnées de A),et que tu puisses enfin terminer ton DM.
Ce n'est qu'une simple proposition.
Amicalement.
Le but en fait est de voir le signe du discriminant en fonction de m.
Selon la valeur de ton discriminant,tu auras plus ou moins de racines réelels,donc plus ou moins d'intersections...
Si tu veux l'ami je te donner la correction de notre exercice afin que tu t'en inspires (car c'est la même chose sauf que toi c'est plus général étant donné que tu n'as pas les coordonnées de A),et que tu puisses enfin terminer ton DM.
Ce n'est qu'une simple proposition.
Amicalement.
A est le point de  d'abscisse 2.
d'abscisse 2.
(Dm) est la droite passant par A et de coefficient directeur m.
(Dm) a pour équation y=mx-2m (je t'épargne ces calculs vu que tu l'a fait )
Les coordonnées des points d'intersections ,s'ils existent, de de Dm sont les solutions du système
de Dm sont les solutions du système
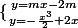
})
-2m(x-2)=0})
(x+2)-2m(x-2)=0})
(-x^2-2x-2m)=0})
(-x^2-2x-2m)=0\Longleftrightarrow x-2=0) ou
ou 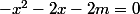 d'après le théorème du produit nul.
d'après le théorème du produit nul.
Etude du trinôme x^+2x+2m=0
a=1,b=2,c=2m
)
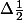 .Le trinôme
.Le trinôme ) n'a pas de racine réelle.L'équation
n'a pas de racine réelle.L'équation (-x^2-2x-2m)=0) n'a qu'une solution:2. A est l'unique point d'intersection de
n'a qu'une solution:2. A est l'unique point d'intersection de  et (Dm).
et (Dm).
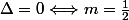 .Le trinôme
.Le trinôme 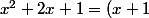^2) a une racine double:-1.
a une racine double:-1.
(Dm) coupe au point A et au point A'(-1;-1,5).
au point A et au point A'(-1;-1,5).
Et tu fais pareil avec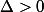 .
.
Après tu fais un tableau de variation avec 2 lignes: 1 ligne avec les valeurs de m, et une ligne avec le nombre de points d'intersection de et (Dm).
et (Dm).
Il y a peut-être des trucs qui t'ont échappés,et je veux bien t'expliquer si c'est le cas.
Bonne chance en tout cas.:++:
Amicalement.
(Dm) est la droite passant par A et de coefficient directeur m.
(Dm) a pour équation y=mx-2m (je t'épargne ces calculs vu que tu l'a fait )
Les coordonnées des points d'intersections ,s'ils existent, de
Etude du trinôme x^+2x+2m=0
a=1,b=2,c=2m
(Dm) coupe
Et tu fais pareil avec
Après tu fais un tableau de variation avec 2 lignes: 1 ligne avec les valeurs de m, et une ligne avec le nombre de points d'intersection de
Il y a peut-être des trucs qui t'ont échappés,et je veux bien t'expliquer si c'est le cas.
Bonne chance en tout cas.:++:
Amicalement.
merci beaucoup!
Merci de tout le temps que tu me consacre, mais je n'y arrive toujours pas!! Dans le cas général j'y arrive pas!! :cry:
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
