Trigonométrie

[maijtm]

Bonjour, alors je vous montre mon exercice :

Dans le plan muni d'un repère orthonormal on donne les points A(-7 ; 1) et B(-4;5) et un point M tel que MA=7 et MB=2. Montrer que MA=MB+BA. Que peut-on en déduire?


Je voulais utilisé Pythagore au début, mais il n'y a pas de carré, donc je ne sais quoi utiliser pour prouvé l'égalité, une aide svp?

Merci d'avance !

[capitaine nuggets]

Bonjour !

Bonjour, alors je vous montre mon exercice :

Dans le plan muni d'un repère orthonormal on donne les points A(-7 ; 1) et B(-4;5) et un point M tel que MA=7 et MB=2. Montrer que MA=MB+BA. Que peut-on en déduire?


Je voulais utilisé Pythagore au début, mais il n'y a pas de carré, donc je ne sais quoi utiliser pour prouvé l'égalité, une aide svp?

Merci d'avance !

As-tu fais un dessin pour t'orienter ?
Trouve les coordonnées du point .

Si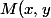 , alors donc .
De la même manière ,.

[maijtm]

Oui j'ai fais un dessin, mais je n'ai pas de compas donc pas très précis.

Donc MA=(x-xA)+(y-yA)

(Pourquoi on utilise cette formule?)

[Kikoo <3 Bieber]

Nein nein nein !

Si tu as a^2=b^2+c^2, je vais te décevoir mais a est bien loin de valoir b+c !
Nous aurons a=sqrt{b^2+c^2} (ou l'opposé) où sqrt{} désigne la racine carrée.

[maijtm]

Nein nein nein !

Si tu as a^2=b^2+c^2, je vais te décevoir mais a est bien loin de valoir b+c !
Nous aurons a=sqrt{b^2+c^2} (ou l'opposé) où sqrt{} désigne la racine carrée.

Mais un carré dans une racine carré sa revient à dire b+c non?

[ampholyte]

Mais un carré dans une racine carré sa revient à dire b+c non?

Pas vraiment.

Si tu as

alors tu obtiens pour x:
ou

Attention à ne pas confondre
et .

Essaye de développer la seconde, tu verras que le résultat que tu obtiens est différente de la première.

Donc dire que est faux.

(Pourquoi on utilise cette formule?)

Je te renvoie à ton cours (si tu en as un), sinon je te conseille de faire un tour sur ce site :
http://www.cmath.fr/2nde/vecteurs/cours.php

Pour revenir à ta question la seule distance que tu as à calculer est la distance AB qui se calcul comme te la montrer capitaine nugget.

edit : coquille corrigé

[Kikoo <3 Bieber]

Ampholyte : il ne s'agit pas de a^2-b^2 mais de a^2+b^2

[ampholyte]

Ampholyte : il ne s'agit pas de a^2-b^2 mais de a^2+b^2

Tout à fait, je sais pas ce qui m'a pris je corrige de suite :briques: et je vais p'tete en profiter pour aller me coucher avant de dire d'autres conneries du genre :mur: .

[maijtm]

Oula j'ai du mal à vous suivre là, je demandais juste la formule qu'il fallait utilisé pour calculer, ce que capitaine nuggets m'a donné, mais j'ai déduis quelque chose de faux et là explication de kikoo <3 bieber, boum néant (ceux qui voient mes topics régulièrement doivent se dire qu'il y a beaucoup le néant dans ma tête), bref je ne comprends pas ce que je dois déduire quand capitaine nuggets a écrit MA= ....

[Kikoo <3 Bieber]

T'inquiètes ;)
Bonne nuit :dodo:

[Kikoo <3 Bieber]

Maijtm : je parlais à Ampholyte ^^

Bon, néant ou pas, va falloir mettre tout ça au clair.
Nous voulons montrer que AM=BM+AB.
On connait AM, on connait BM, boum il faut calculer AB pour vérifier si oui il y a bien égalité.

Or on a les coordonnées de A(xa;ya) et de B(xb;yb). On utilise Pythagore dans le triangle (rectangle en C) ABC où C a pour coordonnées C(xb;ya) (dessine-le tu verras).
On voit bien que AB^2=BC^2+AC^2 ce qui se réécrit en AB^2=(yb-ya)^2+(xb-xa)^2 et tu as l'expression de la norme du vecteur AB.

[maijtm]

Donc j'ai trouvé AB=5

Ah ben oui maintenant je vois :D
Merci beaucoup une fois de plus !!! En espérant réussir mes autres exercices de trigonométrie comme ça j'avancerais bien...

[Kikoo <3 Bieber]

Euhh... Qu'est-ce que tu en déduis au fait ? :)

[maijtm]

Euh... Que les points sont aligné non?

[Kikoo <3 Bieber]

Bien :) inégalité triangulaire toussa quoi... Je vais te laisser tranquille.
Good night

[maijtm]

Rien avoir avec la trigonométrie, mais je l'écris ici pour ne pas réouvrir un topic, comment résoudre algébriquement une equation du second degré... Les sites où je suis allé il n'y a pas la forme que j'ai dans mes exos :

x^2+9=0
(x+1)^2=(x+1)(2x+6)

[maijtm]

Bonne nuit, je vais y aller moi aussi, j'espère demain avoir une réponse pour mes équations :)

[ampholyte]

Rien avoir avec la trigonométrie, mais je l'écris ici pour ne pas réouvrir un topic, comment résoudre algébriquement une equation du second degré... Les sites où je suis allé il n'y a pas la forme que j'ai dans mes exos :

x^2+9=0
(x+1)^2=(x+1)(2x+6)

Pour la première équation on a :

Si tu travailles dans tu n'as pas de solutions car un carré ne peut pas être négatif !!. En revanche si tu travailles dans il faut te rappeler que et donc que tu peux écrire . Tes solutions dans sont donc et .


Pour la seconde équation tu as deux solutions. Soit tu pars en mode "bourrain" tu développes tout et tu "passes tout à gauche" pour résoudre une équation du type (et donc tu résouts les équations directement par le calcul du discriminent et tout le tsointsoin). Soit tu remarques que tu peux factoriser par (x+1) et tu te ramènerais à une forme plus facile à résoudre du type .

Si tu as des questions n'hésite pas,

Bon courage ,)

[maijtm]

Alors je vais tout faire plus tard mais j'aimerais savoir, R c'est réel et C?
A chaque fois qu'il y un carré je peux ramené à x=i?
Comment l'écrire une fois sur papier?

Merci :)

[ampholyte]

Alors je vais tout faire plus tard mais j'aimerais savoir, R c'est réel et C?
A chaque fois qu'il y un carré je peux ramené à x=i?
Comment l'écrire une fois sur papier?

Merci

correspond à l'ensemble des réels et correspond à l'ensemble des complexes.

Une propriété importante est que l'ensemble des réels est inclus dans l'ensemble des complexes.

Un nombre complexe possède une partie réel et une partie imaginaire. On peut l'écrire sous la forme :
z = a + ib (ou z = a + jb, les deux notations existent). Pour faire simple, imagine que pour représenter un nombre réel, on possède un axe centré en 0 (qu'on appellera abscisse pour faire simple). Pour représenter un nombre complexe se représente donc à l'aide d'une abscisse (sa partie réel a) et d'une ordonnée centré autour de 0i = 0 (sa partie imaginaire b).

Dire qu'à chaque fois que tu as un carré tu peux te ramené à x = i est faux. Tout dépend du contexte. Par exemple si tu as tu n'as pas besoin de i pour résoudre cette équation. En revanche quand tu as tu as soit deux solutions dans , (x = 3i et x = -3i), soit aucune solution dans , car un carré ne peut pas être négatif !!.

Pour l'écrire sur le papier tu dois connaître ton ensemble de définition. D'après ce que tu demandes, tu n'as pas du voir l'ensemble des complexes .

Donc pour conclure pour ta première équation tu peux par exemple écrire:
. Un carré est toujours positif dans , donc il n'y a pas de solution pour cette équation.

J'espère que tu as tout compris :we: