Trigonométrie - Programmation

[Neox76]

Bonjour à tous.

Je fais actuellement de la programmation, et je suis tombé malheureusement quelque par ou je dois utiliser de la trigonométrie (si je ne me trompe pas !). J'ai 17 ans et, je n'ai jamais aimé ni compris quoi que ce soit en géométrie, et là malheureusement j'en ai besoin.

Je développe actuellement dans un jeu dit "Open-Source", c'est à dire que les sources sont ouverte, à disposition de qui que ce soit, libre. En gros ce n'est pas moi qui ai créé le jeu, non.

Mon problème c'est que, je dois dessiner une arme avec des lignes (le seul moyen de créer une arme dans ce jeu en programment, c'est cella). Donc j'ai la position du joueur (que j'appelle ici 'a'), la direction de la souris du joueur (donc pour l'instant je peux créer une ligne de la position du joueur à la souris du joueur, 'a' la position du joueur, 'b' la fin de la ligne), mais après avoir fait cette ligne, je dois ajouter une autre ligne qui va de la fin de la ligne ('b') à une direction (qui est inconnue... puisque la direction de la souris du joueur change). J'ai en ma disposition les fonctions sinus et cosinus (qui ont étaient écrites par les créateurs du jeu) mais je ne sais absolument pas m'en servir, je ne sais même pas le quel m'est utile actuellement !

J'ai fais des recherches internet et... ça fait bien 3 jours que je reste bloqué sur ce petit code bien difficile.

En résumé on a 3 points : A = Position du joueur (qui n'est pas vraiment un inconnu *), B = Fin de la ligne qui part de A (qui n'est pas vraiment un inconnu *), C = Fin de la ligne qui part de B, mais que l'ont ne sais pas ou il est exactement car B est une variable (le joueur bouge sa souris !)

J'espère vraiment avoir bien expliqué, je suis disponible pour n'importe quel question et j'espère être dans la bonne parti du forum.

Merci d'avance pour toute aide.

Bonne fin de journée à tous.


* Je dis ça car ce sont des variables, des valeurs qui changent mais que l'ont peut facilement voir à tout moment. Donc ce sont des inconnus, mais pas VRAIMENT.


Edit : J'ai juste besoin de connaître la formule (ou le nom de la formule ; "sinus" "cosinus") pour obtenir l'angle qui va d'un point B à un point C, C qui est un inconnu.

[fatal_error]

slt,

les inconnues qui sont pas vraiment des inconnues, ca s'appèle des paramètres.

Edit : J'ai juste besoin de connaître la formule (ou le nom de la formule ; "sinus" "cosinus") pour obtenir l'angle qui va d'un point B à un point C, C qui est un inconnu.

On ne définit pas un angle avec deux points mais plutot deux segments.
Par exemple l'angle (BA,BC) (qui définit l'angle entre le vecteur BA et le vecteur BC (comme si on voulait l'angle en B du triangle ABC).

Peux-tu etre plus précis?

PS2: on sait pas si tu es en 2d ou en 3d, pe devrais-tu le préciser

[Neox76]

Merci pour le vocabulaire :)

Je ne sais absolument pas comment être plus précis :( Si j'ai des questions, j'y répondrais avec plaisir mais là je ne sais vraiment pas comment être plus précis...

Le jeu est en 2D.

[fatal_error]

ma question est: que cherches tu à calculer: on ne calcule pas un angle avec deux points.

Si tu ne sais pas t'exprimer (vocabulaire etc), tu peux aussi (ce qu'on fait généralement) faire un dessin et adjoindre le lien sur ce forum :)

[Neox76]

D'accord, je vais voir ce que je peux faire =)

[Neox76]

La différence c'est le point C qui devrait être calculé, mais qui là ne l'ai pas. (c'est la même valeur pour les deux, ce que j'ai besoins c'est que les lignes restent pareil, sauf que là elle ne restent pas pareil )

Si ça peut vous aider, je vous publie le code (très court)

Code: Tout sélectionner

vec2 Dir = normalize(vec2(m_OwnerChar->m_Input.m_TargetX, m_OwnerChar->m_Input.m_TargetY)); // La direction de la souris du joueur
    vec2 Start = m_OwnerChar->m_Pos + Dir * 50.0f;
    vec2 To = m_OwnerChar->m_Pos + Dir * 200.0f;

    CNetObj_Laser* pLaser = static_cast(Server()->SnapNewItem(NETOBJTYPE_LASER, m_ID, sizeof(CNetObj_Laser)));
    if(!pLaser)
        return;

    pLaser->m_X = (int)Start.x;// Point A
    pLaser->m_Y = (int)Start.y;
    pLaser->m_FromX = (int)To.x; // La ligne qui va au point B
    pLaser->m_FromY = (int)To.y;
    pLaser->m_StartTick = Server()->Tick();

    CNetObj_Laser* pLaser2 = static_cast(Server()->SnapNewItem(NETOBJTYPE_LASER, m_ID2, sizeof(CNetObj_Laser)));
    if(!pLaser2)
        return;

    pLaser2->m_X = (int)To.x; // Point B
    pLaser2->m_Y = (int)To.y;
    pLaser2->m_FromX = (int)To.x - 50; // La ligne qui va au point C (qui devrait être calculé justement, il ne devrait pas y avoir de - 50 ou de 30 ici
    pLaser2->m_FromY = (int)To.y + 30;
    pLaser2->m_StartTick = Server()->Tick();

    CNetObj_Laser* pLaser3 = static_cast(Server()->SnapNewItem(NETOBJTYPE_LASER, m_ID3, sizeof(CNetObj_Laser)));
    if(!pLaser3)
        return;

    pLaser3->m_X = (int)To.x - 50; // Point C
    pLaser3->m_Y = (int)To.y + 30;
    pLaser3->m_FromX = (int)To.x - 50; // idem, devrait être calculé
    pLaser3->m_FromY = (int)To.y + 30;
    pLaser3->m_StartTick = Server()->Tick();


Vous pouvez aussi regarder ça pour plus de lisibilité http://pastebin.com/7nssNLz5

Je suis toujours disponible pour toutes vos questions...

J'ai ajouté des commentaires pour vous aider, n'hésitez pas à regarder à droite de chaque ligne, si vous voyez un double slash, la suite est un commentaire.

[fatal_error]

Tu veux calculer les coordonnées de C, mais tu dis pas quelle relation il doit satisfaire par rapport à A et B:

Si A a pour coordonnées (0,0)
et B a pour coordonnées (10,10)

pourquoi C de coordonnées (11,13) serait invalide.

Est-ce que l'angle (ABC) est constant (par exemple vaut toujours 30° ou bien vaut toujours 45°)? Je pense que tu sais quand même ce qu'est un angle. Sinon regardes sur le net.

Si l'angle (ABC) n'est pas constant, alors il n'y a pas de solution à ton problème, rien n'empêche de poser C n'importe ou sur un cercle de centre B

[Robic]

Voilà ce que j'ai compris (enfin, deviné, car il faut avouer que ce n'est vraiment pas clair...) : on dispose de trois points A, B, C (donc on dispose de leurs coordonnées je suppose) et il s'agit de calculer l'angle (BA, BC) (d'après les dessins - mais je ne suis pas 100 % sûr).

Une méthode classique est d'utiliser le produit scalaire et le produit vectoriel. À mon époque ce genre de calcul était au programme de terminale mais, depuis, j'ai un peu oublié, néanmoins il me semble que ça ressemble à :





où est l'angle qu'on cherche et 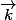est le vecteur unité de la 3è dimension orienté comme il faut.

Le produit scalaire et le produit vectoriel se calculent avec les formules usuelles :



Les normes de vecteurs aussi sont calculables avec les formules usuelles :



Ainsi, on obtient deux formules donnant le cosinus et le sinus :





Si on cherche un angle orienté, donc défini à 360° près, elles sont nécessaires. Si c'est un angle non orienté, une seule formule suffit.

Ensuite, il y a deux façons de procéder :
- On utilise un arc cosinus ou un arc sinus sur l'une des deux variables X ou Y, ce qui donne l'angle à 180° près. Reste à écrire un test à partir de l'autre variable pour connaître l'angle à 360° près.
- On utilise une fonction de type "arctangente étendue", si elle est disponible dans le langage (en C c'est la fonction atan2), en donnant X et Y comme arguments : elle retourne directement l'angle voulu.

[Neox76]

Tu veux calculer les coordonnées de C, mais tu dis pas quelle relation il doit satisfaire par rapport à A et B:

Si A a pour coordonnées (0,0)
et B a pour coordonnées (10,10)

pourquoi C de coordonnées (11,13) serait invalide.

Est-ce que l'angle (ABC) est constant (par exemple vaut toujours 30° ou bien vaut toujours 45°)? Je pense que tu sais quand même ce qu'est un angle. Sinon regardes sur le net.

Si l'angle (ABC) n'est pas constant, alors il n'y a pas de solution à ton problème, rien n'empêche de poser C n'importe ou sur un cercle de centre B

Justement, mon problème est que l'angle est constant (c'est le problème que j'essaye d'expliquer depuis le début, désolé pour mon vocabulaire ^^)

[Neox76]

Voilà ce que j'ai compris (enfin, deviné, car il faut avouer que ce n'est vraiment pas clair...) : on dispose de trois points A, B, C (donc on dispose de leurs coordonnées je suppose) et il s'agit de calculer l'angle (BA, BC) (d'après les dessins - mais je ne suis pas 100 % sûr).

Une méthode classique est d'utiliser le produit scalaire et le produit vectoriel. À mon époque ce genre de calcul était au programme de terminale mais, depuis, j'ai un peu oublié, néanmoins il me semble que ça ressemble à :





où est l'angle qu'on cherche et est le vecteur unité de la 3è dimension orienté comme il faut.

Le produit scalaire et le produit vectoriel se calculent avec les formules usuelles :



Les normes de vecteurs aussi sont calculables avec les formules usuelles :



Ainsi, on obtient deux formules donnant le cosinus et le sinus :





Si on cherche un angle orienté, donc défini à 360° près, elles sont nécessaires. Si c'est un angle non orienté, une seule formule suffit.

Ensuite, il y a deux façons de procéder :
- On utilise un arc cosinus ou un arc sinus sur l'une des deux variables X ou Y, ce qui donne l'angle à 180° près. Reste à écrire un test à partir de l'autre variable pour connaître l'angle à 360° près.
- On utilise une fonction de type "arctangente étendue", si elle est disponible dans le langage (en C c'est la fonction atan2), en donnant X et Y comme arguments : elle retourne directement l'angle voulu.

Merci pour ta réponse =) Mais disons que je ne suis vraiment, VRAIMENT pas alaise avec la géométrie, je vais essayer de comprendre tout ça :hein:

Si vous avez quelques notions de programmation (les schéma comme ça, je n'arrive vraiment pas à les comprendre, désolé :stupid:) il me serait bien utile que vous les écrivez en quelques lignes comme si on l'écrivait dans un programme. (j'arriverais mieux à lire et à comprendre ^^)

[Robic]

Je crois qu'il faudrait expliquer les choses plus clairement. Par exemple j'apprends que l'angle est constant, du coup ma réponse précédente est probablement inappropriée. Et je crois que je n'ai en fait rien compris...

Peut-être que j'ai mal lu. Dans ce cas, est-ce que quelqu'un qui a compris le problème peut l'expliquer ?

[fatal_error]

slt,
robic,

Justement, mon problème est que l'angle est constant (c'est le problème que j'essaye d'expliquer depuis le début, désolé pour mon vocabulaire ^^)

L'angle est constant. Neox76 cherche a calculer les coordonnees du point C, connaissant les points A, B et langle ABC (jimagine qu il connait egalement la longueur BC (ex: 4cm)

Il ne s'agit donc pas de calculer l'angle mais de s'en servir en tant que parametre

[Robic]

Ah OK ! Donc on doit calculer le point C ? Effectivement pour ça il faut connaître la longueur BC.

Dans ce cas on peut procéder ainsi :
1) On place C' sur la droite (BA) tel que BC' = BC.
2) Puis on effectue une rotation d'angle a (j'appelle a l'angle en question).

Ce qui donne :

(Il y a une erreur, corrigée plus loin à 14h49)

1)

2) où [M] est la matrice de rotation d'angle a.

En détail :





en espérant ne pas m'être trompé...

--------
Et voici une fonction en C qui calcule ça :

void calculpoint( double xa, double ya, double xb, double yb, double bc, double angle, double *pxc, double *pyc)

/* Entrée :
- coords de A : xa, ya
- coords de B : xb, yb
- distance BC : bc
- angle (BA, BC) : angle
*/

/* Sortie :
- pxc, pyc : pointeurs sur les coordonnées de C
- utilise
*/

{
double ba ; /* distance BA */
double xcc, ycc ; /* coordonnées du point C' de (BA) tel que BC' = BC */
double xc, yc ; /* coordonnées du point C */

ba = sqrt( (xa - xb) * (xa - xb) + (ya - yb) *(ya - yb) ) ;
xcc = bc * (xa - xb) / ba ;
ycc = bc * (ya - yb) / ba ;
xc = cos( angle ) * xcc - sin( angle ) * ycc ;
yc = sin( angle ) * xcc + cos( angle ) * ycc ;

*pxc = xc ;
*pyc = yc ;
}

(Bien sûr il y a beaucoup de calculs redondants, c'est juste pour faire le lien avec la méthode mathématique.)

[Neox76]

slt,
robic,



L'angle est constant. Neox76 cherche a calculer les coordonnees du point C, connaissant les points A, B et langle ABC (jimagine qu il connait egalement la longueur BC (ex: 4cm)

Il ne s'agit donc pas de calculer l'angle mais de s'en servir en tant que parametre

Voilà c'est exactement ça :we: !

Merci pour vos réponses ! Je vais lire ça dès que j'aurais un peu plus de temps, je dois travailler là

[Neox76]

Ah OK ! Donc on doit calculer le point C ? Effectivement pour ça il faut connaître la longueur BC.

Dans ce cas on peut procéder ainsi :
1) On place C' sur la droite (BA) tel que BC' = BC.
2) Puis on effectue une rotation d'angle a (j'appelle a l'angle en question).

Ce qui donne :

1)

2) où [M] est la matrice de rotation d'angle a.

En détail :





en espérant ne pas m'être trompé...

--------
Et voici une fonction en C qui calcule ça :

void calculpoint( double xa, double ya, double xb, double yb, double bc, double angle, double *pxc, double *pyc)

/* Entrée :
- coords de A : xa, ya
- coords de B : xb, yb
- distance BC : bc
- angle (BA, BC) : angle
*/

/* Sortie :
- pxc, pyc : pointeurs sur les coordonnées de C
- utilise
*/

{
double ba ; /* distance BA */
double xcc, ycc ; /* coordonnées du point C' de (BA) tel que BC' = BC */
double xc, yc ; /* coordonnées du point C */

ba = sqrt( (xa - xb) * (xa - xb) + (ya - yb) *(ya - yb) ) ;
xcc = bc * (xa - xb) / ba ;
ycc = bc * (ya - yb) / ba ;
xc = cos( angle ) * xcc - sin( angle ) * ycc ;
yc = sin( angle ) * xcc + cos( angle ) * ycc ;

*pxc = xc ;
*pyc = yc ;
}

(Bien sûr il y a beaucoup de calculs redondants, c'est juste pour faire le lien avec la méthode mathématique.)

Merci pour cette réponse bien détaillée ! Je vais essayer de reproduire ça et dire ce que ça donne

[Neox76]

Je n'arrive plus à voir le point C (le trait est très long) et l'angle ne reste pas constant. Il y'a sûrement une erreur quelque par ._.
Je vous laisse jeter un oeil au code. (vec2 est un objet "coordonnées" qui contient un float x et un float y)

Code: Tout sélectionner

void CTestLaser::CalculatePos(vec2 A, vec2 B, float DistBC, float Angle, vec2* pC)
{
    const float DistAB = distance(A, B);
    vec2 CC, C;
    //DistAB = sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y));
    CC.x = DistBC * (A.x - B.x) / DistAB;
    CC.y = DistBC * (A.y - B.y) / DistAB;
    C.x = cos(Angle) * CC.x - sin(Angle) * CC.y;
    C.y = sin(Angle) * CC.x + cos(Angle) * CC.y;

    *pC = C;
}

    vec2 Dir = normalize(vec2(m_OwnerChar->m_Input.m_TargetX, m_OwnerChar->m_Input.m_TargetY));
    vec2 Start = m_OwnerChar->m_Pos + Dir * 50;
    vec2 To = m_OwnerChar->m_Pos + Dir * 200.f;
    vec2 To2 = To;
    To2.x -= 50;
    To2.y += 30;
    vec2 C;
    CalculatePos(Start, To, distance(To, To2), 70, &C); // 70 pour l'angle (j'ai mis ça totalement au hasard)


Il existe une fonction "distance(a, b)" qui retourne la distance entre deux coordonnées. Je l'ai tout simplement utilisé ici.

Utiliser sqrt ou pas n'a rien changé, donc je l'ai laissé commenté.

[Robic]

Ah oui, il y a une erreur dans mes calculs, je viens de la trouver !

Je refais tout (l'erreur est indiquée en rouge) :

1) On place C' sur la droite (BA) tel que BC' = BC.
2) Puis on effectue une rotation d'angle a (j'appelle a l'angle en question).

Ce qui donne :

1)

2) où [M] est la matrice de rotation d'angle a.

En détail :

erreur ici (oubli de x_B)
erreur ici (oubli de y_B)
erreur ici (oubli de x_B)
erreur ici (oubli de y_B)
en espérant ne pas m'être trompé...

Plus simplement :





--------
Et voici une fonction en C qui calcule ça :

void calculpoint( double xa, double ya, double xb, double yb, double bc, double angle, double *pxc, double *pyc)

/* Entrée :
- coords de A : xa, ya
- coords de B : xb, yb
- distance BC : bc
- angle (BA, BC) : angle
*/

/* Sortie :
- pxc, pyc : pointeurs sur les coordonnées de C
- utilise
*/

{
double ba ; /* distance BA */
double xbc, ybc ; /* coordonnées du vecteur BC' */
double xc, yc ; /* coordonnées du point C */

ba = sqrt( (xa - xb) * (xa - xb) + (ya - yb) *(ya - yb) ) ;
xbc = bc * (xa - xb) / ba ;
ybc = bc * (ya - yb) / ba ;
xc = xb + cos( angle ) * xbc - sin( angle ) * ybc ;
yc = yb + sin( angle ) * xbc + cos( angle ) * ybc ;

*pxc = xc ;
*pyc = yc ;
}

[Neox76]

J'halucine, ça marche ! Merci beaucoup à vous tous :we: (Il falait que je rajoute la position du joueur pour que ça marche :) ) Merci vraiment ! ça m'aide beaucoup !!

Edit : je viens de voir ton message =) Je vais voir si en le corrigeant, quelque chose va s'améliorer ^^ Pour l'instant je n'ai pas vraiment l'impression que l'angle soit de 70 degré.

Edit2 : Ou est la correction sil te plait ? J'ai un peu de mal à m'y retrouver... et en tout cas, je vous remercie tous pour votre aide =) J'halucine surtout en voyant les calcules et que au final ça fonctionne !

Edit3 : je viens de voir que tu les as coloré, merci =)

[Robic]

Attends, tu vas trop vite ! :we: J'ai mis les erreurs en rouge (j'étais en train de le faire avant ton edit2...)

Moi j'hallucine que tu sois capable de programmer en langage objet mais pas de faire quelques petites opérations de trigonométrie enfantines ! :lol3: (N'ayant jamais rien compris à cette technique - et ce n'est pas faute d'avoir essayé - je considère que ceux qui ont compris la programmation objet sont des génies...)

[Neox76]

Je viens de suivre la correction, il y a une petite erreur, j'ai retiré les corrections de ces deux lignes et là ça fonctionne parfaitement (sinon la ligne va beaucoup trop loin, on ne la voit plus)
xcc = xb + bc * (xa - xb) / ba ;
ycc = yb + bc * (ya - yb) / ba ;

Merci encore =)