Trigonométrie démonstration de sin(a+b)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Yuravin
- Membre Naturel
- Messages: 53
- Enregistré le: 08 Oct 2006, 09:56
-
 par Yuravin » 09 Juil 2007, 20:49
par Yuravin » 09 Juil 2007, 20:49
Salut,
Je cherche un moyen de démontrer : sin(a+b) = sin(a) cos(b) + cos(a) sin(b)
sans passer par la démonstration de cos(a+b) = cos(a) cos(b) - sin(a) sin(b)
Quelqu'un aurait une idée ?
merci a+
-
Cyberlilu
- Membre Naturel
- Messages: 76
- Enregistré le: 04 Juil 2007, 16:10
-
 par Cyberlilu » 09 Juil 2007, 20:53
par Cyberlilu » 09 Juil 2007, 20:53
déjà pour commencer cos(a+b) ne serait pas plutôt égal à cosacosb - sinasinb ???
-
Yuravin
- Membre Naturel
- Messages: 53
- Enregistré le: 08 Oct 2006, 09:56
-
 par Yuravin » 09 Juil 2007, 20:56
par Yuravin » 09 Juil 2007, 20:56
oui c'est rectifié
il faut que j'aille me coucher, ça ne va plus... :)
-
Cyberlilu
- Membre Naturel
- Messages: 76
- Enregistré le: 04 Juil 2007, 16:10
-
 par Cyberlilu » 09 Juil 2007, 20:58
par Cyberlilu » 09 Juil 2007, 20:58
:we: ok sinon pour la démo là tout de suite j'en sais rien désolée!
-
Ledescat
- Membre Naturel
- Messages: 98
- Enregistré le: 08 Juil 2007, 15:13
-
 par Ledescat » 09 Juil 2007, 21:03
par Ledescat » 09 Juil 2007, 21:03
Bonsoir.
Si tu as vu les nombres complexes, tu peux utiliser le fait que:
=\fr{exp{ix}+exp{-ix}}{2} \\sin(x)=\fr{exp{ix}-exp{-ix}}{2i})
Et tu pars des termes de droite pour arriver à ceux de gauche.
Sinon, il doit exister des démonstrations géométriques, mais c'est plus laborieux.
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 09 Juil 2007, 21:03
par emdro » 09 Juil 2007, 21:03
Bonsoir,
Pourquoi ne pas écrire
})
Tu développes à gauche, puis tu extrais les parties imaginaires.
-
Ledescat
- Membre Naturel
- Messages: 98
- Enregistré le: 08 Juil 2007, 15:13
-
 par Ledescat » 09 Juil 2007, 21:05
par Ledescat » 09 Juil 2007, 21:05
emdro a écrit:Bonsoir,
Pourquoi ne pas écrire
})
Tu développes à gauche, puis tu extrais les parties imaginaires.
J'aime mieux comme cela !
-
Yuravin
- Membre Naturel
- Messages: 53
- Enregistré le: 08 Oct 2006, 09:56
-
 par Yuravin » 09 Juil 2007, 21:05
par Yuravin » 09 Juil 2007, 21:05
oui, mais en passant par les formules d'Euler on démontre cos(a+b)
et je voudrais démontrer uniquement sin(a+b)
-
Ledescat
- Membre Naturel
- Messages: 98
- Enregistré le: 08 Juil 2007, 15:13
-
 par Ledescat » 09 Juil 2007, 21:06
par Ledescat » 09 Juil 2007, 21:06
Yuravin a écrit:oui, mais en passant par les formules d'Euler on démontre cos(a+b)
et je voudrais démontrer uniquement sin(a+b)
La technique d'emdro te donne les 2 pour le prix d'un :we: .
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 09 Juil 2007, 21:07
par emdro » 09 Juil 2007, 21:07
Si tu ne regardes que les parties imaginaires, tu n'entendras pas parler des cos !
-
Yuravin
- Membre Naturel
- Messages: 53
- Enregistré le: 08 Oct 2006, 09:56
-
 par Yuravin » 09 Juil 2007, 21:08
par Yuravin » 09 Juil 2007, 21:08
celle-ci me convient
merci a+
Cyberlilu a écrit:Si tu ne regardes que les parties imaginaires, tu n'entendras pas parler des cos !
Tu parles quand même de cos ^^
-
Ledescat
- Membre Naturel
- Messages: 98
- Enregistré le: 08 Juil 2007, 15:13
-
 par Ledescat » 09 Juil 2007, 21:10
par Ledescat » 09 Juil 2007, 21:10
Ma foi...l'art de se compliquer la vie :we:
-
Ledescat
- Membre Naturel
- Messages: 98
- Enregistré le: 08 Juil 2007, 15:13
-
 par Ledescat » 09 Juil 2007, 21:13
par Ledescat » 09 Juil 2007, 21:13
Yuravin a écrit:celle-ci me convient
merci a+
Tu parles quand même de cos ^^
Le calcul avec la méthode d'emdro se fait en 2 lignes, comparé à la page de démonstrations géométriques.
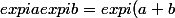} \\(cos(a)+isin(a))(cos(b)+isin(b))=cos(a+b)+isin(a+b) \\cos(a)cos(b)-sin(a)sin(b)+i(sin(a)cos(b)+sin(b)cos(a))=(cos(a+b)+isin(a+b)))
Et en idenfitiant les parties imaginaires, hop :we: .
-
Yuravin
- Membre Naturel
- Messages: 53
- Enregistré le: 08 Oct 2006, 09:56
-
 par Yuravin » 09 Juil 2007, 21:15
par Yuravin » 09 Juil 2007, 21:15
oui mais tu démontres en plus cos
je veux uniquement démontrer sin(a+b)
et sans le théorème de Ptolémée c'est possible ?
-
Cyberlilu
- Membre Naturel
- Messages: 76
- Enregistré le: 04 Juil 2007, 16:10
-
 par Cyberlilu » 09 Juil 2007, 21:18
par Cyberlilu » 09 Juil 2007, 21:18
ça n'a pas vraiment l'air non?? ^^
je confirme la méthode avec complexes largement plus simple et plus facile !!
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 09 Juil 2007, 21:19
par emdro » 09 Juil 2007, 21:19
Yuravin a écrit:Tu parles quand même de cos ^^
Dans la mesure où cos figure dans la formule finale, il est difficile de les éviter vraiment...
D'où te vient ce désamour du cosinus? :happy2:
-
Cyberlilu
- Membre Naturel
- Messages: 76
- Enregistré le: 04 Juil 2007, 16:10
-
 par Cyberlilu » 09 Juil 2007, 21:19
par Cyberlilu » 09 Juil 2007, 21:19
lol oui assez amusante la remarque
-
Cyberlilu
- Membre Naturel
- Messages: 76
- Enregistré le: 04 Juil 2007, 16:10
-
 par Cyberlilu » 09 Juil 2007, 21:20
par Cyberlilu » 09 Juil 2007, 21:20
et puis en suivant cette méthode si tu t'occupes que de la partie imaginaire je vois pas en quoi tu démontres l'autre tu n'as qu'à pas y penser tu verras ^^
-
Ledescat
- Membre Naturel
- Messages: 98
- Enregistré le: 08 Juil 2007, 15:13
-
 par Ledescat » 09 Juil 2007, 21:21
par Ledescat » 09 Juil 2007, 21:21
emdro a écrit:Dans la mesure où cos figure dans la formule finale, il est difficile de les éviter vraiment...
Pas faux, même vrai :we: .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
