Trigonométrie 1erS
17 messages
- Page 1 sur 1
Trigonométrie 1erS
Bonjour,
Voilà nous avons abordé depuis peu le chapitre sur la trigonométrie et j'ai un dm a rendre là dessus sauf que je n'y arrive pas vraiment.. Je ne comprend pas.. J'aimerai donc de l'aide
Voici le sujet en pièce jointe
Merci d'avance
Voilà nous avons abordé depuis peu le chapitre sur la trigonométrie et j'ai un dm a rendre là dessus sauf que je n'y arrive pas vraiment.. Je ne comprend pas.. J'aimerai donc de l'aide
Voici le sujet en pièce jointe
Merci d'avance
- Fichiers joints
-
- Sans titre 6.jpg (45.53 Kio) Vu 543 fois
Re: Trigonométrie 1erS
Voir le cercle trigonométrique.
tout d'abord calculer la vitesse
12 sec pour parcourir 2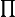 R.,
R.,
arc en radians, tu peux aussi calculer en degrés et même en longueur d'arc.
tout d'abord calculer la vitesse
12 sec pour parcourir 2
arc en radians, tu peux aussi calculer en degrés et même en longueur d'arc.
Re: Trigonométrie 1erS
MABYA a écrit:Voir le cercle trigonométrique.
tout d'abord calculer la vitesse
pour parcourir 2R.,
arc en radians, tu peux aussi calculer en degrés et même en longueur d'arc.
Du coup je trouve :
12 sec -> 2
6sec ->
1sec-> 1/6
30sec -> 5
40sec -> 20/3
57sec -> 19/2
Re: Trigonométrie 1erS
Salut,
On va dire que sur le principe, c'est bon : dans chaque cas tu as donné (en radian comme demandé) une des mesures de l'angle en question.
Sauf que le même angle admet plusieurs mesures différentes et que ce qu'on t'a demandé de donner, c'est la mesure principale de l'angle qui elle, est unique.
1) C'est quoi la définition de la mesure principale d'un angle ?
2) Quand on a une mesure pas forcément principale d'un angle, on fait comment pour en déduire la mesure principale de ce même angle ?
P.S. ça m'arrangerais fortement que tu ait la réponse au moins à la question 1) vu que je sais pas trop ce qu'on raconte au Lycée sur le sujet...
On va dire que sur le principe, c'est bon : dans chaque cas tu as donné (en radian comme demandé) une des mesures de l'angle en question.
Sauf que le même angle admet plusieurs mesures différentes et que ce qu'on t'a demandé de donner, c'est la mesure principale de l'angle qui elle, est unique.
1) C'est quoi la définition de la mesure principale d'un angle ?
2) Quand on a une mesure pas forcément principale d'un angle, on fait comment pour en déduire la mesure principale de ce même angle ?
P.S. ça m'arrangerais fortement que tu ait la réponse au moins à la question 1) vu que je sais pas trop ce qu'on raconte au Lycée sur le sujet...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Trigonométrie 1erS
Ben314 a écrit:Salut,
On va dire que sur le principe, c'est bon : dans chaque cas tu as donné (en radian comme demandé) une des mesures de l'angle en question.
Sauf que le même angle admet plusieurs mesures différentes et que ce qu'on t'a demandé de donner, c'est la mesure principale de l'angle qui elle, est unique.
1) C'est quoi la définition de la mesure principale d'un angle ?
2) Quand on a une mesure pas forcément principale d'un angle, on fait comment pour en déduire la mesure principale de ce même angle ?
P.S. ça m'arrangerais fortement que tu ait la réponse au moins à la question 1) vu que je sais pas trop ce qu'on raconte au Lycée sur le sujet...
La mesure principale est la valeur d'angle comprise dans l'intervalle ]-
Re: Trigonométrie 1erS
A mon avis, ça doit plutôt être dans 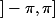 avec
avec  inclus dans l'intervalle (sinon il "manquerais" un angle)
inclus dans l'intervalle (sinon il "manquerais" un angle)
Et comme tu as du le constater, dans tes réponses, il y en a plusieurs dont la valeur n'est pas dans cet intervalle là donc ce n'est pas la bonne réponse.
Comment "rectifie-t-on" le tir dans ce cas là ?
Et comme tu as du le constater, dans tes réponses, il y en a plusieurs dont la valeur n'est pas dans cet intervalle là donc ce n'est pas la bonne réponse.
Comment "rectifie-t-on" le tir dans ce cas là ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Trigonométrie 1erS
Ben314 a écrit:A mon avis, ça doit plutôt être dansavec
inclus dans l'intervalle (sinon il "manquerais" un angle)
Et comme tu as du le constater, dans tes réponses, il y en a plusieurs dont la valeur n'est pas dans cet intervalle là donc ce n'est pas la bonne réponse.
Comment "rectifie-t-on" le tir dans ce cas là ?
Ah oui donc je reprends :
12 sec -> 2
6sec ->
1sec-> 1/6
30sec -> 5
40sec -> 20/3
57sec -> 19/2
Re: Trigonométrie 1erS
C'est bon, sauf le premier vu que  , c'est pas une "valeur principale", sauf que, si tu met à la place la valeur principale correspondante, à savoir 0, la ligne suivante où tu divise par 6 devient un peu n'importe quoi (0/6, ça fait évidement 0).
, c'est pas une "valeur principale", sauf que, si tu met à la place la valeur principale correspondante, à savoir 0, la ligne suivante où tu divise par 6 devient un peu n'importe quoi (0/6, ça fait évidement 0).
Donc a mon avis, tu n'écrit pas cette première ligne et c'est bon.
Après, si ça t'intéresse de comprendre le "pourquoi" le truc déconne au départ, ça vient du fait que la notion (mathématique) d'angle ne colle pas toujours bien avec le problème concret qu'on a.
Pour éviter les radians ou tout autre unité angulaire, si on s'exprime simplement en terme de "nombre de tours tours", au niveau angulaire (i.e. mathématique), faire "trois tours et demi" (= radians), c'est la même chose que de faire "un demi tour" (=
radians), c'est la même chose que de faire "un demi tour" (= radians), mais dans le cas d'un manège, par exemple, bien que les position finale du manège soit les même dans les deux cas (qu'il ait fait 3 tour 1/2 ou bien 1/2 tour), personnellement, je dirais pas que "c'est la même chose" de faire "3 tours et demi de manège" et de faire "1/2 tour de manège".
radians), mais dans le cas d'un manège, par exemple, bien que les position finale du manège soit les même dans les deux cas (qu'il ait fait 3 tour 1/2 ou bien 1/2 tour), personnellement, je dirais pas que "c'est la même chose" de faire "3 tours et demi de manège" et de faire "1/2 tour de manège".
Bref, dans le cas de l'exercice, c'est assez clair que de dire que la grande roue tourne d'un tour en 12 secondes, c'est pas tout à fait pareil que de dire qu'elle tourne de "rien" en 12 seconde.
De même, a mon avis, le fait de dire qu'en 40 secondes, elle a fait\times\!2\pi) radians, c'est à dire 3+1/3 tours me semble être une information plutôt plus pertinente que de dire simplement qu'elle est (à la fin) situé à une position correspondante à 1/3 de tour (qui est la mesure principale de l'angle)
radians, c'est à dire 3+1/3 tours me semble être une information plutôt plus pertinente que de dire simplement qu'elle est (à la fin) situé à une position correspondante à 1/3 de tour (qui est la mesure principale de l'angle)
Donc a mon avis, tu n'écrit pas cette première ligne et c'est bon.
Après, si ça t'intéresse de comprendre le "pourquoi" le truc déconne au départ, ça vient du fait que la notion (mathématique) d'angle ne colle pas toujours bien avec le problème concret qu'on a.
Pour éviter les radians ou tout autre unité angulaire, si on s'exprime simplement en terme de "nombre de tours tours", au niveau angulaire (i.e. mathématique), faire "trois tours et demi" (=
Bref, dans le cas de l'exercice, c'est assez clair que de dire que la grande roue tourne d'un tour en 12 secondes, c'est pas tout à fait pareil que de dire qu'elle tourne de "rien" en 12 seconde.
De même, a mon avis, le fait de dire qu'en 40 secondes, elle a fait
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Trigonométrie 1erS
Ben314 a écrit:C'est bon, sauf le premier vu que, c'est pas une "valeur principale", sauf que, si tu met à la place la valeur principale correspondante, à savoir 0, la ligne suivante où tu divise par 6 devient un peu n'importe quoi (0/6, ça fait évidement 0).
Donc a mon avis, tu n'écrit pas cette première ligne et c'est bon.
Après, si ça t'intéresse de comprendre le "pourquoi" le truc déconne au départ, ça vient du fait que la notion (mathématique) d'angle ne colle pas toujours bien avec le problème concret qu'on a.
Pour éviter les radians ou tout autre unité angulaire, si on s'exprime simplement en terme de "nombre de tours tours", au niveau angulaire (i.e. mathématique), faire "trois tours et demi" (=radians), c'est la même chose que de faire "un demi tour" (=
radians), mais dans le cas d'un manège, par exemple, bien que les position finale du manège soit les même dans les deux cas (qu'il ait fait 3 tour 1/2 ou bien 1/2 tour), personnellement, je dirais pas que "c'est la même chose" de faire "3 tours et demi de manège" et de faire "1/2 tour de manège".
Bref, dans le cas de l'exercice, c'est assez clair que de dire que la grande roue tourne d'un tour en 12 secondes, c'est pas tout à fait pareil que de dire qu'elle tourne de "rien" en 12 seconde.
De même, a mon avis, le fait de dire qu'en 40 secondes, elle a faitradians, c'est à dire 3+1/3 tours me semble être une information plutôt plus pertinente que de dire simplement qu'elle est (à la fin) situé à une position correspondante à 1/3 de tour (qui est la mesure principale de l'angle)
Et pour 60sec j'ai
Re: Trigonométrie 1erS
C'est bien ça :teambs a écrit:Et pour 60sec j'ai
Et comme mesure principale, ça fait ???
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Trigonométrie 1erS
Ben314 a écrit:C'est bien ça :teambs a écrit:Et pour 60sec j'airadians, c'est à dire 5 tours (normal vu qu'on fait un tour toutes les 12 secondes)
Et comme mesure principale, ça fait ???
C'est donc
Re: Trigonométrie 1erS
Non,  n'est pas dans l'intervalle
n'est pas dans l'intervalle 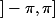 donc ce n'est pas la mesure principale (par contre, c'est bien une des nombreuses mesures de l'angle)
donc ce n'est pas la mesure principale (par contre, c'est bien une des nombreuses mesures de l'angle)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Trigonométrie 1erS
Ben314 a écrit:Non,n'est pas dans l'intervalle
donc ce n'est pas la mesure principale (par contre, c'est bien une des nombreuses mesures de l'angle)
Ah ben c'est
Re: Trigonométrie 1erS
Non plus...
Quand tu as une des (gras + souligné....) mesures d'un angle, pour obtenir les autres mesures du même angle, tu ajoute (ou retranche) autant de fois que tu veut.
autant de fois que tu veut.
Or, on ne peut pas passer de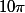 (une des mesures de l'angle) à
(une des mesures de l'angle) à  (valeur que tu propose comme mesure principale) en retranchant un certain nombre (entier) de fois
(valeur que tu propose comme mesure principale) en retranchant un certain nombre (entier) de fois  :
:

Ce qui signifie que sont différentes mesure du même angle.
sont différentes mesure du même angle.
Parmi toutes ces valeurs, quelle est celle appartenant à ? (il y en a une et une seule)
? (il y en a une et une seule)
Quand tu as une des (gras + souligné....) mesures d'un angle, pour obtenir les autres mesures du même angle, tu ajoute (ou retranche)
Or, on ne peut pas passer de
Ce qui signifie que
Parmi toutes ces valeurs, quelle est celle appartenant à
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
