[RESOLU]tracé de courbe avec sinus
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
frxxneoxx
- Membre Naturel
- Messages: 44
- Enregistré le: 04 Aoû 2015, 14:40
-
 par frxxneoxx » 18 Aoû 2016, 16:58
par frxxneoxx » 18 Aoû 2016, 16:58
Bonjour,
J'ai un devoir avec 3 problèmes à résoudre, j'ai réussi les 2 premiers mais je bloque totalement sur le 3ème:
on considère la fonction f définie sur l'intervalle
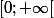
par:
=-0.02e^{-3t} sin(4t))
1. déterminer les valeurs de t appartenant à l'intervalle [0;1.5[ pour lesquelles f(t)=0.
2. Calculer la dérivée de la fonction f. On admet que, pour
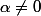
, les équations:
a.sin

+b.cos

=0 et tan

=-b/a
d'inconnue

, ont les mêmes solutions. Déterminer les valeurs approchées, à
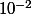
près, des nombre réels t appartenant à l'intervalle [0;1.5[, et annulant f'(t).Pour chaque valeur de t ainsi obtenue, préciser la valeur correspondante de f(t).
3. Déduire des questions 1. et 2. l'allure de la courbe C représentative de f dans le plan rapporté à un repère orthogonal.On prendra 10cm pour une unité en abscisse et 1cm pour 0.002 en ordonnée
J'avoue que dès qu'il y a de la trigo

si vous pouviez me mettre sur la voie. Merci
Modifié en dernier par
frxxneoxx le 19 Aoû 2016, 19:42, modifié 1 fois.
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 18 Aoû 2016, 17:07
par Razes » 18 Aoû 2016, 17:07
=-0.02e^{-3t} sin(4t))
)
est le produit de plusieurs termes.
Lequel des termes peut être nul pour que
=0)
?
-
frxxneoxx
- Membre Naturel
- Messages: 44
- Enregistré le: 04 Aoû 2015, 14:40
-
 par frxxneoxx » 18 Aoû 2016, 17:29
par frxxneoxx » 18 Aoû 2016, 17:29
Razes a écrit:=-0.02e^{-3t} sin(4t))
)
est le produit de plusieurs termes.
Lequel des termes peut être nul pour que
=0)
?
ohhh je dois trouvé la valeur de t qui annule le sinus.
Donc je dois résoudre l'équation :
sin(4t)=0
?
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 18 Aoû 2016, 17:37
par Razes » 18 Aoû 2016, 17:37
Oui
-
frxxneoxx
- Membre Naturel
- Messages: 44
- Enregistré le: 04 Aoû 2015, 14:40
-
 par frxxneoxx » 18 Aoû 2016, 18:40
par frxxneoxx » 18 Aoû 2016, 18:40
=0)
cela revient à résoudre:
sin(4t)=0
ou sin(4t)=sin(0)
soit par inversion trigonométrique sinA= sinB
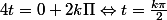
; avec
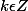
et
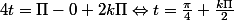
; avec
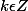
soit S={
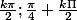
}avec
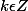
donc l'unique valeur t appartenant à l'intervalle [0;1.5[ pour lesquelles f(t)=0 est:
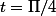
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 18 Aoû 2016, 21:17
par Razes » 18 Aoû 2016, 21:17
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 18 Aoû 2016, 21:22
par Razes » 18 Aoû 2016, 21:22
frxxneoxx a écrit:donc
l'unique valeur t appartenant à l'intervalle [0;1.5[ pour lesquelles f(t)=0 est:
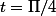
Faux
-
frxxneoxx
- Membre Naturel
- Messages: 44
- Enregistré le: 04 Aoû 2015, 14:40
-
 par frxxneoxx » 19 Aoû 2016, 08:35
par frxxneoxx » 19 Aoû 2016, 08:35
Razes a écrit: frxxneoxx a écrit:donc
l'unique valeur t appartenant à l'intervalle [0;1.5[ pour lesquelles f(t)=0 est:
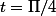
Faux
ah oui j'ai oublié 0

:
donc les valeurs de t appartenant à l'intervalle [0;1.5[ pour lesquelles f(t)=0 sont 0 et
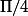
je ne comprends pas la première ligne, je trouve ça moi:
=0)
; Donc:
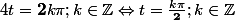
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 19 Aoû 2016, 12:43
par Razes » 19 Aoû 2016, 12:43
Tu as trouvé ça:
frxxneoxx a écrit: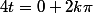
; avec
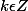
et
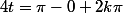
; avec
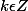
Ce qui équivaut à
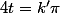
avec
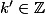
(on a juste regroupé les termes paires et impaires avant de passer à la division)
Pour le signe appartenance utilise
\in au lieu de
\epsilon
-
frxxneoxx
- Membre Naturel
- Messages: 44
- Enregistré le: 04 Aoû 2015, 14:40
-
 par frxxneoxx » 19 Aoû 2016, 13:10
par frxxneoxx » 19 Aoû 2016, 13:10
je suis passé à la question 2. mais je bloque encore:
=-0.02e^{-3t} sin(4t))
Je calcul la dérivée, grâce à la formule u x v = u'v+uv'
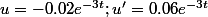
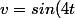 ; v'=4cos(4t))
soit:
 = 0.06e^{-3t}.sin(4t) - 0.08 e^{-3t}.cos(4t))
j'utilise la formule donnée dans l'énoncé
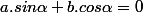
et
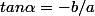
avec:
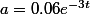
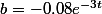
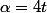
soit
=-(\frac{-0.08e^{-3t}}{0.06e^{-3t}})=\frac{4}{3})
et la je bloque. Je n'arrive pas a trouvé la valeur tangente égal 4/3 pour me retrouver avec une équation du type tanA=tanB.
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 19 Aoû 2016, 14:02
par Razes » 19 Aoû 2016, 14:02
frxxneoxx a écrit:soit
=-(\frac{-0.08e^{-3t}}{0.06e^{-3t}})=\frac{4}{3})
et la je bloque. Je n'arrive pas a trouvé la valeur tangente égal 4/3 pour me retrouver avec une équation du type tanA=tanB.
Pourquoi? tu ne peux pas simplifier ton expression:
=-\frac{-0.08*e^{-3t}}{0.06*e^{-3t}})
L'affaire
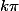
est règlée?
-
frxxneoxx
- Membre Naturel
- Messages: 44
- Enregistré le: 04 Aoû 2015, 14:40
-
 par frxxneoxx » 19 Aoû 2016, 14:40
par frxxneoxx » 19 Aoû 2016, 14:40
Razes a écrit:Pourquoi? tu ne peux pas simplifier ton expression:
=-\frac{-0.08*e^{-3t}}{0.06*e^{-3t}})
L'affaire
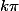
est règlée?
Pourquoi je ne peux pas simplifier ?
Quand j'ai vu la direction que prenait la résolution je pensais simplifier au maximum l'équation pour arriver sous la forme de tanA=tanB pour ensuite résoudre avec a=b+Pi. Mais je n'arrive pas à déterminer quels angles permettent d'obtenir une tangente qui vaut 1.33333.
oui l'affaire KPi est réglée merci. J'ai plus que la 2. est j'ai fini mon devoir.
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 19 Aoû 2016, 18:06
par Razes » 19 Aoû 2016, 18:06
Pour calculer l'angle, il y a plusieurs méthodes:
- Tables trigonométriques
- Calculatrice en utilisant la fonction inverse
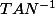
- Calculateur Online
http://www.rapidtables.com/calc/math/Tan_Calculator.htm tu spécifie si c'est en degré ou en radian. = 53.1300336°
- ....
-
frxxneoxx
- Membre Naturel
- Messages: 44
- Enregistré le: 04 Aoû 2015, 14:40
-
 par frxxneoxx » 19 Aoû 2016, 19:23
par frxxneoxx » 19 Aoû 2016, 19:23
Razes a écrit:Pour calculer l'angle, il y a plusieurs méthodes:
- Tables trigonométriques
- Calculatrice en utilisant la fonction inverse
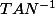
- Calculateur Online
http://www.rapidtables.com/calc/math/Tan_Calculator.htm tu spécifie si c'est en degré ou en radian. = 53.1300336°
- ....
donc juste en utilisant la fonction inverse tangente je peux résoudre l'équation

je suis parti dans un délire ....
mais de cette façon je ne trouve qu'une solution !
tan(4t)=1.33333
=0.927294rad)
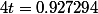
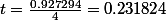
soit0.23 à
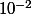
près
Vu que f'(t) oscille, je devrais trouvé beaucoup de valeur de t qui annule f'(t) et ensuite réduire les réponses à l'intervalle d'étude or ça n'est pas mon cas. il doit me manquer une étape car 0.23 est une réponse correct ...
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
-
frxxneoxx
- Membre Naturel
- Messages: 44
- Enregistré le: 04 Aoû 2015, 14:40
-
 par frxxneoxx » 19 Aoû 2016, 19:41
par frxxneoxx » 19 Aoû 2016, 19:41
ne m'a pris de vitesse.
donc toutes les valeurs annulant f'(t) sont:
0.231824+kPi/4
et 0.231824-kPi/4
et les valeurs annulant f'(t) et étant dans l'intervalle [0;1.5[ sont:
s=[0.23;1.02] à
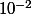
près
Ok merci beaucoup Razes pour ton aide. Je n'aurais jamais réussi sans toi

-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 19 Aoû 2016, 22:25
par Razes » 19 Aoû 2016, 22:25
frxxneoxx a écrit:0.231824+kPi/4
et 0.231824-kPi/4
Pas nécessaire d'écrire les deux options car
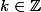
dont peut être négatif ou positif.
C'est avec plaisir. Bonne continuation
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
par:
, les équations:
+b.cos
=0 et tan
=-b/a
, ont les mêmes solutions. Déterminer les valeurs approchées, à
près, des nombre réels t appartenant à l'intervalle [0;1.5[, et annulant f'(t).Pour chaque valeur de t ainsi obtenue, préciser la valeur correspondante de f(t).

