.
3 messages
- Page 1 sur 1
Re: Dérivée de la fonction x*sqrt(x) avec (f(a+h)-f(a))/h
par capitaine nuggets » 22 Avr 2019, 11:37
Salut !
Multiplie au numérateur et au dénominateur par la quantité conjuguée\sqrt{a+h}+a\sqrt{a})
de \sqrt{a+h}-a\sqrt{a})
.
Au numérateur tu risques d'avoir besoin de savoir/montrer que^3=a^3+3a^2h+3ah^2+h^3)
.
A la fin, après simplifications, tu dois trouver= \frac 3 2 \sqrt a)
.
Multiplie au numérateur et au dénominateur par la quantité conjuguée
Au numérateur tu risques d'avoir besoin de savoir/montrer que
A la fin, après simplifications, tu dois trouver
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Dérivée de la fonction x*sqrt(x) avec (f(a+h)-f(a))/h
par aymanemaysae » 22 Avr 2019, 12:33
Bonjour;
1.
Une autre façon de faire :
-f(a)}{h}=\dfrac{(a+h)\sqrt{a+h}-a\sqrt a}{h}=\dfrac{\sqrt{a+h}^3-\sqrt{a}^3}{h})
(\sqrt{a+h}^2+\sqrt a\sqrt{a+h}+\sqrt{a}^2)}{h})
(a+h+\sqrt a\sqrt{a+h}+a)}{h}=\dfrac{(\sqrt{a+h}-\sqrt{a})(2a+h+\sqrt a\sqrt{a+h})}{h})
(\sqrt{a+h}+\sqrt{a})(2a+h+\sqrt a\sqrt{a+h})}{h(\sqrt{a+h}+\sqrt{a})})
(2a+h+\sqrt a\sqrt{a+h})}{h(\sqrt{a+h}+\sqrt{a})}=\dfrac{(a+h-a)(2a+h+\sqrt a\sqrt{a+h})}{h(\sqrt{a+h}+\sqrt{a})})
}{h(\sqrt{a+h}+\sqrt{a})}=\dfrac{2a+h+\sqrt a\sqrt{a+h}}{\sqrt{a+h}+\sqrt{a}})
.
2.
-f(a)}{h} = \underset{h\rightarrow 0}{lim} \dfrac{2a+h+\sqrt a\sqrt{a+h}}{\sqrt{a+h}+\sqrt{a}})
)
.
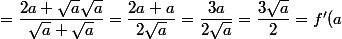Pour l'ensemble de dérivabilité, je crois que c'est immédiat .
1.
Une autre façon de faire :
2.
Pour l'ensemble de dérivabilité, je crois que c'est immédiat .
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :