√x + √y = √xy
63 messages
- Page 1 sur 4 - 1, 2, 3, 4
√x + √y = √xy
Bonjour, la question est dans le titre : trouveriez nombre de solutions de cette équations (solutions dans N)
J'ai tenté une démarche mais ne suis bloqué : vu qu'il ne faut pas résoudre l'équation mais bien seulement le nombre de solutions, j'ai voulu transformer chaque membre en une fonction, isoler y, et trouver les intersections entre ces fonctions. Mais le problème c'est que je n'arrive pas à isoler y.
J'ai tenté une démarche mais ne suis bloqué : vu qu'il ne faut pas résoudre l'équation mais bien seulement le nombre de solutions, j'ai voulu transformer chaque membre en une fonction, isoler y, et trouver les intersections entre ces fonctions. Mais le problème c'est que je n'arrive pas à isoler y.
Re: √x + √y = √xy
Rmq : l'exercice s'adresse à des gens ne connaissant pas les équations diophantiennes ^^
Re: √x + √y = √xy
En bidouillant l'expression de départ, on aboutit à ^2})
Ceci implique que est nécessairement un carré parfait notons le
est nécessairement un carré parfait notons le 
Il s'en suit :
^2}=(\frac{n}{n-1})^2)
On peut s'en doute conclure en disant que le nombre de solutions correspond au nombre de valeurs de tels que
tels que 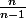 soit un entier.
soit un entier.
Ceci implique que
Il s'en suit :
On peut s'en doute conclure en disant que le nombre de solutions correspond au nombre de valeurs de
Re: √x + √y = √xy
salut
(\sqrt y - 1) = 1)
or les seuls diviseurs de 1 dans Z sont 1 et -1 ...

or les seuls diviseurs de 1 dans Z sont 1 et -1 ...

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: √x + √y = √xy
C'est la démonstration qui me paraissait la plus clair, mais un point me gène, c'est de considérer quezygomatique a écrit:salut
or les seuls diviseurs de 1 dans Z sont 1 et -1 ...
Obligatoire de démontrer que
Re: √x + √y = √xy
Bonjour zygomatique, comment as tu trouver ton équation finale ? Y A t il une technique pour y arriver ?
Re: √x + √y = √xy
De plus es,ne faut il pas tenir compte que √ est une racine, ce qui implique 2 solutions opposés ?
Re: √x + √y = √xy
pour tous réels a et b :: (b - 1) = 1)
ou encore on l'identité remarquable ::(b + 1) - 1) ou encore
ou encore (b - 1) - 1)
ensuite pour revenir à l'équation initiale :
1/ évidemment les racines carrées imposent que leurs arguments respectifs soient positifs
2/ se rappeler que parfois pour résoudre une équation dans R on travaille dans C ...
mais
3/ dans N (ou Z) je ne cherche que des facteurs entiers donc ou
ou 
et ces deux systèmes ont le bon gout de me donner des solutions entières ...
à comparer par exemple avec l'équation à résoudre dans Z ...
à résoudre dans Z ...
REM : l'addition est une loi interne dans N donc
donc
ou encore on l'identité remarquable ::
ensuite pour revenir à l'équation initiale :
1/ évidemment les racines carrées imposent que leurs arguments respectifs soient positifs
2/ se rappeler que parfois pour résoudre une équation dans R on travaille dans C ...
mais
3/ dans N (ou Z) je ne cherche que des facteurs entiers donc
et ces deux systèmes ont le bon gout de me donner des solutions entières ...
à comparer par exemple avec l'équation
REM : l'addition est une loi interne dans N donc
donc
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: √x + √y = √xy
Je ne comprends pas,qu'est ce qui implique quoi ? C'est le signe dune racine carré ou d'un radical ? En outre, ou trouver toutes ces formules ?
Re: √x + √y = √xy
Aerosun006 a écrit:Bonjour, la question est dans le titre : trouveriez nombre de solutions de cette équations (solutions dans N)
J'ai tenté une démarche mais ne suis bloqué : vu qu'il ne faut pas résoudre l'équation mais bien seulement le nombre de solutions, j'ai voulu transformer chaque membre en une fonction, isoler y, et trouver les intersections entre ces fonctions. Mais le problème c'est que je n'arrive pas à isoler y.
Eliminons le cas trivial : x=y=0. Puisqu'il s'agit seulement de donner le nombre de solutions, l'équation se transforme en :
On a donc : 1
Modifié en dernier par Pseuda le 28 Juil 2016, 18:57, modifié 2 fois.
Re: √x + √y = √xy
Donc
Remplaçons
il y a deux possibilité
*
*
Injectons cela dans l'équation initiale, nous obtenons
Donc les cas possibles sont
*
*
Re: √x + √y = √xy
pourquoi faire compliqué quand on peut faire simple ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: √x + √y = √xy
zygomatique a écrit:pourquoi faire compliqué quand on peut faire simple ....
J'étais le 1er à dire que ta démonstration est clair mais tu n'as pas répondu à ma question concernant un point important.
Razes a écrit:C'est la démonstration qui me paraissait la plus clair, mais un point me gène, c'est de considérer quezygomatique a écrit:salut
or les seuls diviseurs de 1 dans Z sont 1 et -1 ...
et
sont dans
sans justification, ou plus simplement de considérer
et
sont dans
Obligatoire de démontrer queet
sont des carrés.
il te faut démontrer que
Re: √x + √y = √xy
Razes a écrit:;
Donc; c'est juste pur simplifier l'écriture
Remplaçonsdans l’équation initiale, nous obtenons
il y a deux possibilité
*; dans ce cas
*Donc
; Le seul diviseur de
dans
est, donc
; d’où
Injectons cela dans l'équation initiale, nous obtenons
Donc les cas possibles sontou
*donc
et
*donc
et
Bonsoir,
Re: √x + √y = √xy
J'ai oublié de noter cela
^2=1+\frac{2k+1}{k^2}\in \mathbb{N})
Donc ; Donc
; Donc  divise
divise 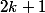 ce qui implique que
ce qui implique que  divise
divise  , d’où
, d’où 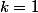
Donc^2=2^2=4)
Ce qui permet de raccourcir la démonstration.
Donc
Donc
Ce qui permet de raccourcir la démonstration.
Re: √x + √y = √xy
Donc
Remplaçons
il y a deux possibilité
Cas 1)
Cas 2)
Donc
Donc
63 messages
- Page 1 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
