√x + √y = √xy
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 12 Sep 2016, 08:35
par chan79 » 12 Sep 2016, 08:35
Razes a écrit: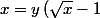^2\Rightarrow y\mid x)
salut
il faudrait être sûr que
^2)
est un entier, il me semble
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 12 Sep 2016, 09:24
par Razes » 12 Sep 2016, 09:24
Tu as raison
chan79. Voici le récapitulatif de la démonstration:
Récapitulatif de la démonstration:Soient

, tel que:
 (1)a)
(1)a) \Rightarrow x=y\left (\sqrt{x}-1 \right )^2\Rightarrow x=y\left ( x+1-2\sqrt{x} \right )=ky)
avec


donc
\in\mathbb{Q}\Rightarrow \sqrt{x}\in\mathbb{Q}\Rightarrow x)
est un carré de plus nous avons

; D'où
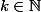
; donc:
 b)
b) 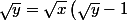\Rightarrow y=x\left (\sqrt{y}-1 \right )^2\Rightarrow y=x\left ( y+1-2\sqrt{y} \right )=kx)
avec


donc
\in\mathbb{Q}\Rightarrow \sqrt{y}\in\mathbb{Q}\Rightarrow y)
est un carré de plus nous avons

; D'où
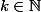
; donc:
 c) Conclusion:
c) Conclusion: \land \left (x\mid y \right )\Leftrightarrow y=x)
Reportons ce résultat dans l'équation (1), nous obtenons:
=0)
Nous avons donc deux solutions:

d'où
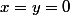
ou

d'où
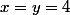 CQFD
CQFD

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 12 Sep 2016, 19:57
par zygomatique » 12 Sep 2016, 19:57
tant qu'à démonter que x et y sont des carrés je préfère ma démo ...
mais j'apprécie pleinement cette démo ::
Razes a écrit:Tiens, tiens, un sujet qui reviens! (
Je ne reviens pas aux précédentes démonstrations)
Soient

, tel que:
 (1)
(1)\Rightarrow x=y\left (\sqrt{x}-1 \right )^2\Rightarrow y\mid x)
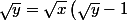\Rightarrow y=x\left (\sqrt{y}-1 \right )^2\Rightarrow x\mid y)
Ceci entraine que:

Reportons ce résultat dans l'équation (1), nous obtenons:
=0)
Nous avons donc deux solutions:

d'où
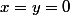
ou

d'où
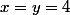
CQFD
qui est quasiment du même acabit que ma factorisation (classique dans les entiers)

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
, tel que:
(1)
d'où
d'où