Bonjour, j'ai du mal à résoudre mon DM de maths, je n'ai vraiment le sens de la logique mais j'essaie d'y travailler pourriez-vous m'aider ? Merci
Exercice 1
On donne les points A(-3 ;2) : B(2 ;4) ; C(5 ;-3) relativement au repère (O I J)
Dans chacun des cas suivants, trouver les coordonnées (x ;y) du point M
a) ABCM est un parallélogramme
b) M est le point de l'axe des abscisses tel que les vecteurs AB et CM sont colinéaires
c) M est l'image de C par la symétrie de centre B
J'ai énormément de mal à résoudre cet exercice !
Exercice 2 (deux démonstrations pour montrer que deux droites sont parallèles)
Soit ABCD un rectangle. Le point E appartient au segment [AB] tel que AE=2/3AB et le point F appartient au segment [BC] tel que BF = 1/3 BC
Méthode 1 : 1) Dans le repère (A ; vecteur AB ; vecteur AB), quelles sont les coordonnées des point A, B, C, D, E, F ?
2) Démontrer que les vecteurs AC et EF sont colinéaires. Que pont on en déduire ?
Méthode 2 : Démontrer vectoriellement que le vecteur EF = 1/3vecteurAC. Que peut-on en déduire ?
Méthode 1 : 1. A (0;0) B (1;0) C (1;1) D (0;1) E (2/3 ; 0) F (1;1/3)
2. On calcul les oordonnées des vecteurAC et EF : vecteurAC = (xC-xa)
vecteurAC (1-0)
vecteurAC(1)
(yc-ya) = (1-0) = 1 (1;1)
vecteurEF (xf-xe) = vecteurEF (1-2/3)
= vecteurEF 1/3
(yf-ye) 1/3-0 = 1/3
On utilise les produit en croix : 1*1/3 = 1-3 et 1*1/3 = 1/3
Les produites en croix sont égaux. Les vecteurs AC et EF sont colinéaire, donc (AC) et (EF) sont parallèles
Méthode 2 : vecteurEF = vecteurEB +vecteurBF = vecteurEB + 1/3 vecteurBC = 1/3vecteurAB + 1/3vecteurBC = 1/3 (vecteurAB + vecteurBC) = 1/3vecteurAC
Exercice 3
(O I J) est un repère orthonormé du plan
On considère les points R (-9 ;-1), E (-6 ;-6), C (9 ; 3), T (6 ; 8)
1) Placer ces points dans le repère et conjecturer la nature du quadrilatère RECT
(J'ai conjecturé que RECT est rectangle)
2) Calculer les distances RE, EC, CT, et RT
3) Ces distances permettent-elles de conclure sur la nature de quadrilatère RECT ?
4) Quel autre calcul de distance doit-on faire pour conclure ? Quel théorème utilise- t on alors ?
1) Je peux conjecturer que le quadrilatère est un parallélogramme.
2) RE =racinede34
J'ai fait la même chose pour les autres : EC = racinede306
CT = racinede34
RT = racinede306
3) Oui, on peut conlure que le quadrilatère est un parallélogramme.
4) Il faut calculer les diagonales ?
Dm
6 messages
- Page 1 sur 1
Salut !
a) Définition : est un parallélogramme si et seulement si
est un parallélogramme si et seulement si  .
.
b) Si le point de coordonnées
de coordonnées ) appartient à l'axe des abscisses alors
appartient à l'axe des abscisses alors  .
.
De plus, si les vecteurs et
et 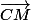 sont colinéaires, alors il existe un réel
sont colinéaires, alors il existe un réel  (que tu seras amené à déterminer) tel que
(que tu seras amené à déterminer) tel que  .
.
c) est l'image de
est l'image de  par la symétrie de centre
par la symétrie de centre  équivaut à
équivaut à  .
.
Trace la figure pour t'en convaincre :++:
@+
katty29 a écrit:(...)
Exercice 1
On donne les points A(-3 ;2) : B(2 ;4) ; C(5 ;-3) relativement au repère (O I J)
Dans chacun des cas suivants, trouver les coordonnées (x ;y) du point M
a) ABCM est un parallélogramme
b) M est le point de l'axe des abscisses tel que les vecteurs AB et CM sont colinéaires
c) M est l'image de C par la symétrie de centre B
J'ai énormément de mal à résoudre cet exercice !
(...)
a) Définition :
b) Si le point
De plus, si les vecteurs
c)
Trace la figure pour t'en convaincre :++:
@+
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Salut !
a) Définition :est un parallélogramme si et seulement si
.
b) Si le pointde coordonnées
appartient à l'axe des abscisses alors
.
De plus, si les vecteurset
sont colinéaires, alors il existe un réel
(que tu seras amené à déterminer) tel que
.
c)est l'image de
par la symétrie de centre
équivaut à
.
Trace la figure pour t'en convaincre :++:
@+
Merci beaucoup ! Mes autres exercices sont-ils corrects ?
katty29 a écrit:
Exercice 2 (deux démonstrations pour montrer que deux droites sont parallèles)
Soit ABCD un rectangle. Le point E appartient au segment [AB] tel que AE=2/3AB et le point F appartient au segment [BC] tel que BF = 1/3 BC
Méthode 1 : 1) Dans le repère (A ; vecteur AB ; vecteur AB), quelles sont les coordonnées des point
Ne serait-ce pas plutôt le repère
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
augustin29 a écrit:salut katty,
pour la 4 de l'exercice 4 moi j'ai calculé la diagonale ET et utilisé dans le triangle TCE la réciproque du théorème de Pythagore afin de dire que le triangle TCE etait rectangle et donc dire que la figure etait un rectangle!
voila, on se voit a la rentre :p
ptdr ! vieux pseudo pourri ^^ De toutes façon, je l'ai finit, je suis trop forte et trop intelligente (et je connais quelqu'un de fort en maths)
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
