Théorème des valeurs intermédiaires

[LostInMathWorld]

Bonjour! J'ai très prochainement un examen en math et je suis quelques peu perdu sous la tonne de travail à faire...
J'aurais aimé savoir si vous pouviez m'expliquer comment prouver le théorème des valeurs intermédiaires!
Merci d'avance !

[busard_des_roseaux]

vlà une démo vite fait

I)
f continue sur [a;b]
f(a) 0
alors f s'annule sur [a;b]

demo
on fait la dichotomie (tomeo=couper, dicho=en deux)

on teste
si , c gagné . f s'annule

si on remplace l'intervalle [a;b]
par et on recommence

si on remplace l'intervalle [a;b]
par et on recommence

on construit ainsi par récurrence une suite emboitée
de segments de longueur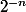
par compacité de [a;b] l'intersection de cette suite emboitée
de segments n'est pas vide. elle contient un point z.
f(z)=0 car f(z) positif et négatif.

II)
ensuite si f continue prend les valeurs m et M
et
on applique le théorème précedent à

[busard_des_roseaux]

autre démo possible

f(a)0

soit [TEX]E=\{ x \in [a;b] / f(x)0 , on trouve une contradiction en utilisant la continuité de f
en z , point intérieur de [a;b]

[Nightmare]

Salut,

autre méthode usuelle : Si on cherche un antécédent à y par f, il peut être intéressant de considérer . Quitte à remplacer f par son opposé, on peut supposer que f(a) et f(b) sont rangés dans le même ordre que a et b si bien que A est non vide et majoré, donc admet une borne sup. Je te laisse montrer que cette borne sup ne peut être autre qu'un antécédent de y par f.

Edit : Grillé.