DM taux de variation (problème)

[nixso75]

Bonjour, j'ai un dm de maths sur les taux de variations. J'ai déjà réussi les trois premiers exercices mais il me manque la 4, 5 et 6 auxquels je ne comprends pas très bien.

À la 3 j'ai trouvé: Un = 4n-92

À la 4 on me demande de déterminer le sens de variation de la suite (Un)

À la 5 on me demande de calculer les 5 premiers termes de la suite (Un)

Et à la 6: En interprétant les termes de la suite (Un), émettre une conjecture sur le sens de variation de Fn sur [1;3] si n<5

Pour Fn j'avais trouvé 9n-193.

Merci d'avance pour votre aide !

[mathelot]

A la question 4) calcule la différence u(n+1)-u(n)

[hdci]

... Et à la 5), qu'est-ce que vous ne comprenez pas N Vous avez 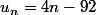et on vous demande de calculer les 5 premier terme. Quels sont les 5 premiers termes ?

[Black Jack]

Bonjour,

Tu devrais écrire l'énoncé en entier.

Tes réponses me poussent à penser que tu t'es planté.

En effet, l'énoncé suggère que tu as besoin des termes de Un pour trouver le sens de variation de Fn sur [1;3] si n<5

Et si on a effectivement Fn = 9n-193 ... alors c'est plus que très suspect.

[nixso75]

A la question 4) calcule la différence u(n+1)-u(n)

Donc en sachant que Un = 4n-92

Je fais 4n-92 + 1- 4n-92 ?

[hdci]

Si ,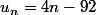

Comment calculez-vous ? (en remplaçant n par 0)
Comment calculez-vous ? (en remplaçant n par 1)
Comment calculez-vous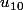 ? (en remplaçant... ?)
Comment calculez-vous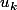 , pour n'importe quel k dont on vous donnerait la valeur ? (en remplaçant ... ?)

Donc, comment calculez-vous ???

, ce n'est pas u indice n auquel on ajoute 1, c'est u indice (n+1)

[nixso75]

Si ,

Comment calculez-vous ? (en remplaçant n par 0)
Comment calculez-vous ? (en remplaçant n par 1)
Comment calculez-vous ? (en remplaçant... ?)
Comment calculez-vous , pour n'importe quel k dont on vous donnerait la valeur ? (en remplaçant ... ?)

Donc, comment calculez-vous ???

, ce n'est pas u indice n auquel on ajoute 1, c'est u indice (n+1)

Ahh! Donc pour un+1 c'est juste 4+1-92 ou plutôt 4n+1-92

[nixso75]

Donc pour la 4 j'ai fait ça:

https://zupimages.net/up/21/01/6b7d.jpg

[nixso75]

Heu pour la 5 plutôt

[WillyCagnes]

bjr,
U(n)=4n-92

et U(n+1)=4(n+1)-92

ensuite tu peux calculer U(n+1)-U(n)=?

[nixso75]

A la question 4) calcule la différence u(n+1)-u(n)

Donc je fais 4+1-92 - 4-92 ce qui est égale à 1 ?

[nixso75]

bjr,
U(n)=4n-92

et U(n+1)=4(n+1)-92

ensuite tu peux calculer U(n+1)-U(n)=?

Salut willy bah je fais 4+1-92 - 4-92 ce qui fait 1 ?

[nixso75]

J'ai trouvé 4+1-92-4-92 = 5-92 - 4-92 = - 87 - (-86) = 1

[nixso75]

Heu non-87- (-88) pardon

[nixso75]

J'ai trouvé 1 mais ils disent de déterminer le sens de variation. Étant donné que 1>0 alors il est croissant c'est ça ?

[nixso75]

Bonjour,

Tu devrais écrire l'énoncé en entier.

Tes réponses me poussent à penser que tu t'es planté.

En effet, l'énoncé suggère que tu as besoin des termes de Un pour trouver le sens de variation de Fn sur [1;3] si n<5

Et si on a effectivement Fn = 9n-193 ... alors c'est plus que très suspect.

Bah j'ai écrit en entier je te jure

[hdci]

J'ai trouvé 1 mais ils disent de déterminer le sens de variation. Étant donné que 1>0 alors il est croissant c'est ça ?

Le raisonnement est correct (la différence est positive donc c'est croissant).
Mais le calcul est archi faux.

bjr,
U(n)=4n-92

et U(n+1)=4(n+1)-92

ensuite tu peux calculer U(n+1)-U(n)=?

Salut willy bah je fais 4+1-92 - 4-92 ce qui fait 1 ?

Mais où est passé la variable n dans le calcul en rouge ???

Bah j'ai écrit en entier je te jure

Sûrement pas car on ne sait pas ce qu'est Fn dans l'énoncé indiqué en début de post.

[nixso75]

J'ai trouvé 1 mais ils disent de déterminer le sens de variation. Étant donné que 1>0 alors il est croissant c'est ça ?

Le raisonnement est correct (la différence est positive donc c'est croissant).
Mais le calcul est archi faux.

bjr,
U(n)=4n-92

et U(n+1)=4(n+1)-92

ensuite tu peux calculer U(n+1)-U(n)=?

Salut willy bah je fais 4+1-92 - 4-92 ce qui fait 1 ?

Mais où est passé la variable n dans le calcul en rouge ???

Bah j'ai écrit en entier je te jure

Sûrement pas car on ne sait pas ce qu'est Fn dans l'énoncé indiqué en début de post.

Bah quoi je devais garder n ? Je croyais qu'il fallait le remplacé

Dans ce cas c'est 4n+1-92- 4n-92 = 1n?

Et pour la 6 Fn est 9n-193

Et la consigne c'est: "En interprétant les termes de la suite (Un), émettre une conjecture sur le sens de variation de Fn sur [1;3] si n<5."

[nixso75]

De Fn: Montrer que l'image de 3 par Fn est 9n-193.
Ensuite: montrer que le taux de variation de Fn entre 1 et 3 est 4n-92

[nixso75]

???