Symétrie axiale

[Zweig]

Bonjour,

A l'instar des rotations, translations etc ..., existe-t-il une formule pour la symétrie axiale dans le plan complexe ?

Merci.

[leon1789]

oui, en utilisant la conjugaison complexe

[Zweig]

C'est-à-dire ? Tu veux parler du cas particulier de la symétrie avec comme droite l'axe des abscisses ? Mais si la droite est une droite quelconque ? J'avais pensé à utiliser l'angle entre l'axe des abscisses justement et la droite par rapport à laquelle on effectue la symétrie ... :hum:

[Huppasacee]

Il serait intéressant , par des considérations géométriques , de voir si on peut trouver une formule

par exemple symétrie par rapport à une droite passant par A (a ) faisant un angle theta avec l'axe des réels ?

[leon1789]

par exemple symétrie par rapport à une droite passant par A (a ) faisant un angle theta avec l'axe des réels ?

exactement !

La symétrie axiale de référence est justement la conjugaison complexe.
Ensuite, on prend un axe et on le tourne et/ou on translate...

[leon1789]

C'est-à-dire ? Tu veux parler du cas particulier de la symétrie avec comme droite l'axe des abscisses ? Mais si la droite est une droite quelconque ? J'avais pensé à utiliser l'angle entre l'axe des abscisses justement et la droite par rapport à laquelle on effectue la symétrie ... :hum:

Exemple simple : symétrie par rapport à iR

z -> z / i (envoie iR sur R)
puis z -> conj. de z (symetrie)
puis z -> z . i (envoie R sur iR)

ce qui donne tout simplement z -> - conj. de z

[Huppasacee]

z -> z / i (envoie iR sur R)
puis z -> conj. de z (symetrie)
puis z -> z . i (envoie R sur iR)

suivons le même cheminement , mais maintenant avec une droite faisant un angle
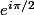
donc ici , au lieu de i ( ), on prendra

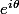
et on terminera par une translation

[Zweig]

Bon, on montre sauf erreur que l'image d'un point par l'axe avec et est :

[axiome]

Bonsoir,
Personnellement, j'avais appris ceci :

L'expression d'une symétrie axiale (d'équation ) est :

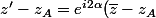où est le point d'intersection de l'axe avec l'axe des abscisses et

[Zweig]

Bon, j'ai vérifié en utilisant la propriété comme quoi une similitude qui fixe deux points est soit une réflexion soit l'identité (on vérifie que si A n'est pas confondu avec B, alors ma transformation n'est pas l'identité) : il se trouve que ma formule fixe A et B.