Suites et log
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Norma
- Membre Relatif
- Messages: 227
- Enregistré le: 18 Jan 2017, 00:11
-
 par Norma » 14 Mai 2017, 16:12
par Norma » 14 Mai 2017, 16:12
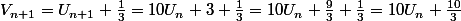
Et
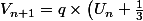= 10\left(U_{n}+\frac{1}{3} \right))
Dons la suite est géométrique, de raison 10
On ne dit pas une telle histoire d’amour, on la chante comme ça et merde à l’amour courtois ! Les temps changent. Quelle leçon!
Héloïse, Ouille! Jean Teulé

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 14 Mai 2017, 16:13
par Lostounet » 14 Mai 2017, 16:13
Ben voilà tu as compris...

J'espère que c'est devenu moins laborieux...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Norma
- Membre Relatif
- Messages: 227
- Enregistré le: 18 Jan 2017, 00:11
-
 par Norma » 14 Mai 2017, 16:14
par Norma » 14 Mai 2017, 16:14
Lostounet a écrit:Ben voilà tu as compris...

J'espère que c'est devenu moins laborieux...
Ca se compliquera un jour ou l'autre ! je vais tenter de refaire la suite stationnaire
On ne dit pas une telle histoire d’amour, on la chante comme ça et merde à l’amour courtois ! Les temps changent. Quelle leçon!
Héloïse, Ouille! Jean Teulé

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 14 Mai 2017, 16:15
par Lostounet » 14 Mai 2017, 16:15
Il faut avant tout comprendre ce que c'est qu'une suite stationnaire.
Que veut dire suite stationnaire pour toi?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Norma
- Membre Relatif
- Messages: 227
- Enregistré le: 18 Jan 2017, 00:11
-
 par Norma » 14 Mai 2017, 16:19
par Norma » 14 Mai 2017, 16:19
Lostounet a écrit:Il faut avant tout comprendre ce que c'est qu'une suite stationnaire.
Que veut dire suite stationnaire pour toi?
Une suite stationnaire c'est une suite où chaque terme est équivalent et où on démontre alors que
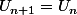
, la suite n'évolue à aucun moment
Laetidom, je n'avais pas vu ta réponse!!! Merci pour tes précisons!!Modifié en dernier par
Norma le 14 Mai 2017, 16:25, modifié 1 fois.
On ne dit pas une telle histoire d’amour, on la chante comme ça et merde à l’amour courtois ! Les temps changent. Quelle leçon!
Héloïse, Ouille! Jean Teulé

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 14 Mai 2017, 16:21
par Lostounet » 14 Mai 2017, 16:21
C'est cela. Stationnaire signifie que la suite ne bouge pas: tous les termes sont égaux.
Donc supposons U(n) est stationnaire, alors si 4U(n+1)=3U(n)+2
Et que U(n+1)=U(n) on peut écrire une égalité satisfaite par U(n) non?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Norma
- Membre Relatif
- Messages: 227
- Enregistré le: 18 Jan 2017, 00:11
-
 par Norma » 14 Mai 2017, 16:24
par Norma » 14 Mai 2017, 16:24
Lostounet a écrit:C'est cela. Stationnaire signifie que la suite ne bouge pas: tous les termes sont égaux.
Donc supposons U(n) est stationnaire, alors si 4U(n+1)=3U(n)+2
Et que U(n+1)=U(n) on peut écrire une égalité satisfaite par U(n) non?
J'ai
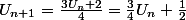
On ne dit pas une telle histoire d’amour, on la chante comme ça et merde à l’amour courtois ! Les temps changent. Quelle leçon!
Héloïse, Ouille! Jean Teulé

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 14 Mai 2017, 16:26
par Lostounet » 14 Mai 2017, 16:26
Okay mais il faut aussi traduire le fait que U(n+1)=U(n)
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Norma
- Membre Relatif
- Messages: 227
- Enregistré le: 18 Jan 2017, 00:11
-
 par Norma » 14 Mai 2017, 16:32
par Norma » 14 Mai 2017, 16:32
Lostounet a écrit:Okay mais il faut aussi traduire le fait que U(n+1)=U(n)
Dans le cours on dit que si q=1 la suite est stationnaire, ducoup on peut pas démontrer que q=1?
On ne dit pas une telle histoire d’amour, on la chante comme ça et merde à l’amour courtois ! Les temps changent. Quelle leçon!
Héloïse, Ouille! Jean Teulé

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 14 Mai 2017, 16:36
par Lostounet » 14 Mai 2017, 16:36
C'est une bonne question
Si une suite est géométrique de raison 1 alors elle est stationnaire... certes.
Mais ici (Un) n'est pas géométrique (elle ne possède pas de raison q!)
La méthode à utiliser est de trouver Un= à quel nombre
Continue ton idée du post précédent. Si U(n+1)=3/4U(n)+1/2
Et que U(n+1)=U(n)
C'est que alors: U(n)=3/4U(n)+1/2
Que vaut donc U(n)?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Norma
- Membre Relatif
- Messages: 227
- Enregistré le: 18 Jan 2017, 00:11
-
 par Norma » 14 Mai 2017, 16:42
par Norma » 14 Mai 2017, 16:42
Lostounet a écrit:C'est une bonne question
Si une suite est géométrique de raison 1 alors elle est stationnaire... certes.
Mais ici (Un) n'est pas géométrique (elle ne possède pas de raison q!)
La méthode à utiliser est de trouver Un= à quel nombre
Continue ton idée du post précédent. Si U(n+1)=3/4U(n)+1/2
Et que U(n+1)=U(n)
C'est que alors: U(n)=3/4U(n)+1/2
Que vaut donc U(n)?
Bah si je remplace U(n) par 3/4U(n)+1/2 on en fini jamais...
Et r doit être égal à 0 alors
On ne dit pas une telle histoire d’amour, on la chante comme ça et merde à l’amour courtois ! Les temps changent. Quelle leçon!
Héloïse, Ouille! Jean Teulé

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 14 Mai 2017, 17:00
par Lostounet » 14 Mai 2017, 17:00
Si a=b
Et a= c donc b=c
Si U(n+1)=3/4U(n)+1/2
Et U(n+1)=U(n)
Donc 3/4U(n)+1/2=U(n)
Donc U(n)-3/4U(n)=1/2
Donc 1/4U(n)=1/2
Donc Un=....
Alors si Un stationnaire, pour tout n, U(n)=...
De quel r tu parles..
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Norma
- Membre Relatif
- Messages: 227
- Enregistré le: 18 Jan 2017, 00:11
-
 par Norma » 14 Mai 2017, 17:08
par Norma » 14 Mai 2017, 17:08
Lostounet a écrit:Si a=b
Et a= c donc b=c
Si U(n+1)=3/4U(n)+1/2
Et U(n+1)=U(n)
Donc 3/4U(n)+1/2=U(n)
Donc U(n)-3/4U(n)=1/2
Donc 1/4U(n)=1/2
Donc Un=....
Alors si Un stationnaire, pour tout n, U(n)=...
De quel r tu parles..
Un est stationnaire pour U(n)=1/2 * 4/1 = 2
Ducoup quand on me demande pour quelle valeur de U0 la suite est stationnaire, c'est pour U0=2?!
ben r, la raison.. si la suite n'est pas géométrique, elle est arithmétique non? donc je ne comprends pas quand est-ce qu'on utilise la propriété qui dit que si r=0 la suite est stationnaire.
On ne dit pas une telle histoire d’amour, on la chante comme ça et merde à l’amour courtois ! Les temps changent. Quelle leçon!
Héloïse, Ouille! Jean Teulé

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 14 Mai 2017, 17:10
par Lostounet » 14 Mai 2017, 17:10
Une suite peut être ni arithmétique, ni géométrique. C'est des cas particuliers de suites.
C'est comme les polygones. Un polygone ça peut être un triangle ou un rectangle ou un losange, mais ça peut être un hexagone ou autre chose...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Norma
- Membre Relatif
- Messages: 227
- Enregistré le: 18 Jan 2017, 00:11
-
 par Norma » 14 Mai 2017, 17:20
par Norma » 14 Mai 2017, 17:20
Histoire d'encore moins s'y retrouver.. Donc U0=2 ?
Je vais calculer les termes
U0=-1
U1= 3/4 * (-1) + 1/2 = -1/4
U2 = 3/4 * (-1/4) + 1/2 = 5/16
U3 = 3/4 * - (5/16) + 1/2 = 47/64
On ne dit pas une telle histoire d’amour, on la chante comme ça et merde à l’amour courtois ! Les temps changent. Quelle leçon!
Héloïse, Ouille! Jean Teulé

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 14 Mai 2017, 17:26
par Lostounet » 14 Mai 2017, 17:26
Norma a écrit:Histoire d'encore moins s'y retrouver.. Donc U0=2 ?
Je vais calculer les termes
U0=-1
U1= 3/4 * (-1) + 1/2 = -1/4
U2 = 3/4 * (-1/4) + 1/2 = 5/16
U3 = 3/4 * - (5/16) + 1/2 = 47/64
Tu dis U0 = 2 puis U0 = -1 ?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Norma
- Membre Relatif
- Messages: 227
- Enregistré le: 18 Jan 2017, 00:11
-
 par Norma » 14 Mai 2017, 17:28
par Norma » 14 Mai 2017, 17:28
Lostounet a écrit: Norma a écrit:Histoire d'encore moins s'y retrouver.. Donc U0=2 ?
Je vais calculer les termes
U0=-1
U1= 3/4 * (-1) + 1/2 = -1/4
U2 = 3/4 * (-1/4) + 1/2 = 5/16
U3 = 3/4 * - (5/16) + 1/2 = 47/64
Tu dis U0 = 2 puis U0 = -1 ?
Je fais les questions de l'exercice, dans le 1 on me demande pour quelle valeur de U0 la suite est stationnaire, et dans le 2 on me demande de calculer les termes en partant de U0=-1
On ne dit pas une telle histoire d’amour, on la chante comme ça et merde à l’amour courtois ! Les temps changent. Quelle leçon!
Héloïse, Ouille! Jean Teulé

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 14 Mai 2017, 17:33
par Lostounet » 14 Mai 2017, 17:33
Ok il reste donc la 4) seulement.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Norma
- Membre Relatif
- Messages: 227
- Enregistré le: 18 Jan 2017, 00:11
-
 par Norma » 14 Mai 2017, 17:36
par Norma » 14 Mai 2017, 17:36
Il n'y a que trois questions dans exercice ?! La 3 c'est ce que tu m'as expliqué avec la suite géométrique et les ptits exercices que tu m'as donné. Tu vois autre chose?
On ne dit pas une telle histoire d’amour, on la chante comme ça et merde à l’amour courtois ! Les temps changent. Quelle leçon!
Héloïse, Ouille! Jean Teulé

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 14 Mai 2017, 17:38
par Lostounet » 14 Mai 2017, 17:38
Norma a écrit:Il n'y a que trois questions dans exercice ?! La 3 c'est ce que tu m'as expliqué avec la suite géométrique et les ptits exercices que tu m'as donné. Tu vois autre chose?
" En déduire l'expression de Un en fonction de n."
Non? Tu l'as faite?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités