Bonjour a tous et merci d'avance de m'aider pour un exercice qui me pose problème
voici l'énoncé
Soit u0 =1 et un+1 = 2un-5 pour tout entier naturel.
On pose vn = 5 un pour tout n ;) 0.
1. Calculer les 5 premiers termes de la suite (vn).
2. Quelle est la nature de la suite (vn) ?
3. Exprimer vn puis un en fonction de n
Ce que j'ai calculer pour le moment:
1) sachant que: un+1 = 2un-5 on en déduit que un = 2un-4
je demontre que un est une suite arithmétique:
un+1 - un= 2un-5 - (2un - 4)
un+1 - un= 2un-5 - 2un +4
un+1 - un= -1
soit un est une suite arithmétique de raison r=-1
soit v0= 5-1=4
soit v1= 5-2=3
soit v2= 5-3=2
soit v3= 5-4=1
soit v4= 5-5=0
2) je definis la nature de la suite (vn):
soit vn+1=5-un soit est egale à 5-(2un-4+1) soit 5-(2un-3)
on calcule vn+1 - vn
on obtient:
5-(2un-3) - (5 un)
-un+3
la suite n'est donc pas arithmétique ni géométrique.
(je ne suis absolument pas sure de mes calculs)
3)
vn(n)=5 (2n-5)
un(n)=2n - 4
Je ne suis absolument pas sure de mes résultats et j'espère que vous pourrez m'aider surtout pour la question 2 et 3 dont je ne suis pas sure.
merci d'avance
Suites 1 ere S
9 messages
- Page 1 sur 1
Salut !
J'ai pas bien saisis comment tu comprenais les questions qu'on te pose.
1°) Pour tout ,
,  .
.
Donc calculer les cinq premiers termes de la suite (v_n) revient à calculer et
et 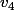 .
.
v_0=5-u_0=4, v_1=5-u_1=5-(2u_0-5)=5-(2-5)=8, v_2=... , je te laisse poursuivre :++:
2°) Dans cette question, il "faut" que la suite) soit particulière (arithmétique, géométrique en général). Sans cela, on pourrait difficilement répondre sans indications complémentaires, à la question suivantes :+++:
soit particulière (arithmétique, géométrique en général). Sans cela, on pourrait difficilement répondre sans indications complémentaires, à la question suivantes :+++:
Calcule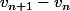 ou
ou 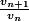 .
.
pbongrand a écrit:Bonjour a tous et merci d'avance de m'aider pour un exercice qui me pose problème
voici l'énoncé
Soit u0 =1 et un+1 = 2un-5 pour tout entier naturel.
On pose vn = 5 un pour tout n0.
1. Calculer les 5 premiers termes de la suite (vn).
2. Quelle est la nature de la suite (vn) ?
3. Exprimer vn puis un en fonction de n
Ce que j'ai calculer pour le moment:
1) sachant que: un+1 = 2un-5 on en déduit que un = 2un-4
je demontre que un est une suite arithmétique:
un+1 - un= 2un-5 - (2un - 4)
un+1 - un= 2un-5 - 2un +4
un+1 - un= -1
soit un est une suite arithmétique de raison r=-1
soit v0= 5-1=4
soit v1= 5-2=3
soit v2= 5-3=2
soit v3= 5-4=1
soit v4= 5-5=0
2) je definis la nature de la suite (vn):
soit vn+1=5-un soit est egale à 5-(2un-4+1) soit 5-(2un-3)
on calcule vn+1 - vn
on obtient:
5-(2un-3) - (5 un)
-un+3
la suite n'est donc pas arithmétique ni géométrique.
(je ne suis absolument pas sure de mes calculs)
3)
vn(n)=5 (2n-5)
un(n)=2n - 4
Je ne suis absolument pas sure de mes résultats et j'espère que vous pourrez m'aider surtout pour la question 2 et 3 dont je ne suis pas sure.
merci d'avance
J'ai pas bien saisis comment tu comprenais les questions qu'on te pose.
1°) Pour tout
Donc calculer les cinq premiers termes de la suite (v_n) revient à calculer
v_0=5-u_0=4, v_1=5-u_1=5-(2u_0-5)=5-(2-5)=8, v_2=... , je te laisse poursuivre :++:
2°) Dans cette question, il "faut" que la suite
Calcule
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Bonjour a tous et merci d'avance de m'aider pour un exercice qui me pose problème
voici l'énoncé
Soit u0 =1 et un+1 = 2un-5 pour tout entier naturel.
On pose vn = 5 un pour tout n 0.
0.
1. Calculer les 5 premiers termes de la suite (vn).
2. Quelle est la nature de la suite (vn) ?
3. Exprimer vn puis un en fonction de n
Ce que j'ai calculer pour le moment:
1) sachant que: un+1 = 2un-5 on en déduit que un = 2un-4
je demontre que un est une suite arithmétique:
un+1 - un= 2un-5 - (2un - 4)
un+1 - un= 2un-5 - 2un +4
un+1 - un= -1
soit un est une suite arithmétique de raison r=-1
soit v0= 5-1=4
V1=5-u1=5-(2u0-5)=8
soit v1= 5-2=3
v2=5-u2=5-(2u1-5)=16
soit v2= 5-3=2
v3=5-u3=5-(2u2-5)=32
soit v3= 5-4=1
v4=5-u4=5-(2u3-5)=64
soit v4= 5-5=0
On conjecture qu'il s' agit d'une suite geometrique de raison 2.
2) je definis la nature de la suite (vn):
soit vn+1=5-un soit est egale à 5-(2un-4+1) soit 5-(2un-3)
on calcule vn+1 - vn
on obtient:
5-(2un-3) - (5 un)
-un+3
la suite n'est donc pas arithmétique ni géométrique.
(je ne suis absolument pas sure de mes calculs)
3)
vn(n)=5 (2n-5)
un(n)=2n - 4
Je ne suis absolument pas sure de mes résultats et j'espère que vous pourrez m'aider surtout pour la question 2 et 3 dont je ne suis pas sure.
merci d'avance[/quote]
voici l'énoncé
Soit u0 =1 et un+1 = 2un-5 pour tout entier naturel.
On pose vn = 5 un pour tout n
1. Calculer les 5 premiers termes de la suite (vn).
2. Quelle est la nature de la suite (vn) ?
3. Exprimer vn puis un en fonction de n
Ce que j'ai calculer pour le moment:
1) sachant que: un+1 = 2un-5 on en déduit que un = 2un-4
je demontre que un est une suite arithmétique:
un+1 - un= 2un-5 - (2un - 4)
un+1 - un= 2un-5 - 2un +4
un+1 - un= -1
soit un est une suite arithmétique de raison r=-1
soit v0= 5-1=4
V1=5-u1=5-(2u0-5)=8
soit v1= 5-2=3
v2=5-u2=5-(2u1-5)=16
soit v2= 5-3=2
v3=5-u3=5-(2u2-5)=32
soit v3= 5-4=1
v4=5-u4=5-(2u3-5)=64
soit v4= 5-5=0
On conjecture qu'il s' agit d'une suite geometrique de raison 2.
2) je definis la nature de la suite (vn):
soit vn+1=5-un soit est egale à 5-(2un-4+1) soit 5-(2un-3)
on calcule vn+1 - vn
on obtient:
5-(2un-3) - (5 un)
-un+3
la suite n'est donc pas arithmétique ni géométrique.
(je ne suis absolument pas sure de mes calculs)
3)
vn(n)=5 (2n-5)
un(n)=2n - 4
Je ne suis absolument pas sure de mes résultats et j'espère que vous pourrez m'aider surtout pour la question 2 et 3 dont je ne suis pas sure.
merci d'avance[/quote]
Bnjour a tous et merci d'avance de m'aider pour un exercice qui me pose problème
voici l'énoncé
Soit u0 =1 et un+1 = 2un-5 pour tout entier naturel.
On pose vn = 5 un pour tout n 0.
0.
1. Calculer les 5 premiers termes de la suite (vn).
2. Quelle est la nature de la suite (vn) ?
3. Exprimer vn puis un en fonction de n
Ce que j'ai calculer pour le moment:
1) sachant que: un+1 = 2un-5 on en déduit que un = 2un-4
je demontre que un est une suite arithmétique:
un+1 - un= 2un-5 - (2un - 4)
un+1 - un= 2un-5 - 2un +4
un+1 - un= -1
soit un est une suite arithmétique de raison r=-1
soit v0= 5-1=4
soit v1= 5-2=3
soit v2= 5-3=2
soit v3= 5-4=1
soit v4= 5-5=0
2) je definis la nature de la suite (vn):
Suite géométriques ssi Vn+1/Vn=constante
Vn+1/Vn=(5-Un+1)/(5-Un)=constante
soit vn+1=5-un soit est egale à 5-(2un-4+1) soit 5-(2un-3)
on calcule vn+1 - vn
on obtient:
5-(2un-3) - (5 un)
-un+3
la suite n'est donc pas arithmétique ni géométrique.
(je ne suis absolument pas sure de mes calculs)
3)
vn(n)=5 (2n-5)
un(n)=2n - 4
Je ne suis absolument pas sure de mes résultats et j'espère que vous pourrez m'aider surtout pour la question 2 et 3 dont je ne suis pas sure.
merci d'avance[/quote]
voici l'énoncé
Soit u0 =1 et un+1 = 2un-5 pour tout entier naturel.
On pose vn = 5 un pour tout n
1. Calculer les 5 premiers termes de la suite (vn).
2. Quelle est la nature de la suite (vn) ?
3. Exprimer vn puis un en fonction de n
Ce que j'ai calculer pour le moment:
1) sachant que: un+1 = 2un-5 on en déduit que un = 2un-4
je demontre que un est une suite arithmétique:
un+1 - un= 2un-5 - (2un - 4)
un+1 - un= 2un-5 - 2un +4
un+1 - un= -1
soit un est une suite arithmétique de raison r=-1
soit v0= 5-1=4
soit v1= 5-2=3
soit v2= 5-3=2
soit v3= 5-4=1
soit v4= 5-5=0
2) je definis la nature de la suite (vn):
Suite géométriques ssi Vn+1/Vn=constante
Vn+1/Vn=(5-Un+1)/(5-Un)=constante
soit vn+1=5-un soit est egale à 5-(2un-4+1) soit 5-(2un-3)
on calcule vn+1 - vn
on obtient:
5-(2un-3) - (5 un)
-un+3
la suite n'est donc pas arithmétique ni géométrique.
(je ne suis absolument pas sure de mes calculs)
3)
vn(n)=5 (2n-5)
un(n)=2n - 4
Je ne suis absolument pas sure de mes résultats et j'espère que vous pourrez m'aider surtout pour la question 2 et 3 dont je ne suis pas sure.
merci d'avance[/quote]
capitaine nuggets a écrit:Salut !
J'ai pas bien saisis comment tu comprenais les questions qu'on te pose.
1°) Pour tout,
.
Donc calculer les cinq premiers termes de la suite (v_n) revient à calculeret
.
v_0=5-u_0=4, v_1=5-u_1=5-(2u_0-5)=5-(2-5)=8, v_2=... , je te laisse poursuivre :++:
2°) Dans cette question, il "faut" que la suitesoit particulière (arithmétique, géométrique en général). Sans cela, on pourrait difficilement répondre sans indications complémentaires, à la question suivantes :+++:
Calculeou
.
Bonjour pbongrand,
Tes calculs sont faux.
Les 5 premières valeurs de
On le démontre :
Porte cette valeur de
Bnjour a tous et merci d'avance de m'aider pour un exercice qui me pose problème
voici l'énoncé
Soit u0 =1 et un+1 = 2un-5 pour tout entier naturel.
On pose vn = 5 un pour tout n 0.
0.
1. Calculer les 5 premiers termes de la suite (vn).
2. Quelle est la nature de la suite (vn) ?
3. Exprimer vn puis un en fonction de n
Ce que j'ai calculer pour le moment:
1) sachant que: un+1 = 2un-5 on en déduit que un = 2un-4
je demontre que un est une suite arithmétique:
un+1 - un= 2un-5 - (2un - 4)
un+1 - un= 2un-5 - 2un +4
un+1 - un= -1
soit un est une suite arithmétique de raison r=-1
soit v0= 5-1=4
soit v1= 5-2=3
soit v2= 5-3=2
soit v3= 5-4=1
soit v4= 5-5=0
2) je definis la nature de la suite (vn):
Suite géométriques ssi Vn+1/Vn=constante
Vn+1/Vn=(5-Un+1)/(5-Un)=(5-2Un+5)/(5-Un)=2=constante
Donc Un est une suite geometrique de raison ...
soit vn+1=5-un soit est egale à 5-(2un-4+1) soit 5-(2un-3)
on calcule vn+1 - vn
on obtient:
5-(2un-3) - (5 un)
-un+3
la suite n'est donc pas arithmétique ni géométrique.
(je ne suis absolument pas sure de mes calculs)
3)
vn(n)=5 (2n-5)
un(n)=2n - 4
Je ne suis absolument pas sure de mes résultats et j'espère que vous pourrez m'aider surtout pour la question 2 et 3 dont je ne suis pas sure.
merci d'avance[/quote]
voici l'énoncé
Soit u0 =1 et un+1 = 2un-5 pour tout entier naturel.
On pose vn = 5 un pour tout n
1. Calculer les 5 premiers termes de la suite (vn).
2. Quelle est la nature de la suite (vn) ?
3. Exprimer vn puis un en fonction de n
Ce que j'ai calculer pour le moment:
1) sachant que: un+1 = 2un-5 on en déduit que un = 2un-4
je demontre que un est une suite arithmétique:
un+1 - un= 2un-5 - (2un - 4)
un+1 - un= 2un-5 - 2un +4
un+1 - un= -1
soit un est une suite arithmétique de raison r=-1
soit v0= 5-1=4
soit v1= 5-2=3
soit v2= 5-3=2
soit v3= 5-4=1
soit v4= 5-5=0
2) je definis la nature de la suite (vn):
Suite géométriques ssi Vn+1/Vn=constante
Vn+1/Vn=(5-Un+1)/(5-Un)=(5-2Un+5)/(5-Un)=2=constante
Donc Un est une suite geometrique de raison ...
soit vn+1=5-un soit est egale à 5-(2un-4+1) soit 5-(2un-3)
on calcule vn+1 - vn
on obtient:
5-(2un-3) - (5 un)
-un+3
la suite n'est donc pas arithmétique ni géométrique.
(je ne suis absolument pas sure de mes calculs)
3)
vn(n)=5 (2n-5)
un(n)=2n - 4
Je ne suis absolument pas sure de mes résultats et j'espère que vous pourrez m'aider surtout pour la question 2 et 3 dont je ne suis pas sure.
merci d'avance[/quote]
tototo a écrit:Bnjour a tous et merci d'avance de m'aider pour un exercice qui me pose problème
voici l'énoncé
Soit u0 =1 et un+1 = 2un-5 pour tout entier naturel.
On pose vn = 5 un pour tout n0.
1. Calculer les 5 premiers termes de la suite (vn).
2. Quelle est la nature de la suite (vn) ?
3. Exprimer vn puis un en fonction de n
Ce que j'ai calculer pour le moment:
1) sachant que: un+1 = 2un-5 on en déduit que un = 2un-4
je demontre que un est une suite arithmétique:
un+1 - un= 2un-5 - (2un - 4)
un+1 - un= 2un-5 - 2un +4
un+1 - un= -1
soit un est une suite arithmétique de raison r=-1
soit v0= 5-1=4
soit v1= 5-2=3
soit v2= 5-3=2
soit v3= 5-4=1
soit v4= 5-5=0
2) je definis la nature de la suite (vn):
Suite géométriques ssi Vn+1/Vn=constante
Vn+1/Vn=(5-Un+1)/(5-Un)=(5-2Un+5)/(5-Un)=2=constante
Donc Un est une suite geometrique de raison ...
soit vn+1=5-un soit est egale à 5-(2un-4+1) soit 5-(2un-3)
on calcule vn+1 - vn
on obtient:
5-(2un-3) - (5 un)
-un+3
la suite n'est donc pas arithmétique ni géométrique.
(je ne suis absolument pas sure de mes calculs)
3)
vn(n)=5 (2n-5)
un(n)=2n - 4
Je ne suis absolument pas sure de mes résultats et j'espère que vous pourrez m'aider surtout pour la question 2 et 3 dont je ne suis pas sure.
merci d'avance
tototo
Qu'est-ce que ce jeu débile ?
vas-tu finir d'emm... les gens ?
Carpate a écrit:tototo
Qu'est-ce que ce jeu débile ?
vas-tu finir d'emm... les gens ?
Je dois m'excuser car je n'avais pas vu que tototo répondait dans le texte même du message de pbongrand sans signaler sa contribution par une couleur ou une mise en italique.
Et puis qu'est-ce que c'est que cette idée bizarre de ne pas répondre à l'emplacement prévu pour la réponse !
Normalement le logiciel du forum refuse une réponse trop courte ...
Et 3 réponses identiques sur ce mode à 9h21, 9h25, 9h43 !
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
