Bonjour à tous, je coince sur un court exo qui traite de la recurrence double. Voici la consigne:
Soit Un la suite définie par U0 = 0 et U1 = 1 et Un+2= 2Un+1-Un.
Calculer U2 U3 et U4. Démontrer par récurrence que Un= n pour tout n apprtient à N.
La démonstration de la double récurrence me pose problème, pourriez vous m'aider ?
Merci, Ladislas
Suite et récurrence double
4 messages
- Page 1 sur 1
ce que tu veux montrer est 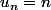
Initialisation de la récurrence : c'est une récurrence "double" donc il faut initialiser avec deux termes :
Ici, on a bien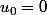 et
et 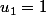
Démonstration au rang n+2 :
On suppose que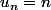 et
et 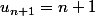 (c'est pour ça qu'on a initialisé avec 2 termes)
(c'est pour ça qu'on a initialisé avec 2 termes)
Alors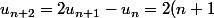-n=n+2)
Donc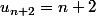 , c'est ce que l'on voulait démontrer
, c'est ce que l'on voulait démontrer
Conclusion
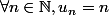
Initialisation de la récurrence : c'est une récurrence "double" donc il faut initialiser avec deux termes :
Ici, on a bien
Démonstration au rang n+2 :
On suppose que
Alors
Donc
Conclusion
Bonjour
Initialisation :
Un = n est vraie aux rangs 0 et 1 (U0=0 et U1=1)
Hérédité :
Hypothèse de récurrence : Supposons Un=n vraie aux rangs k et k+1
c'est à dire Uk=k et Uk+1=k+1
Par hypothèse, Uk+2=2Uk+1 - Uk donc
Uk+2=2(k+1) - k = 2k + 2 - k = k + 2
Si Un=n est vraie aux rangs k et k+1 alors elle est vraie au rang k+2
Or elle est vraie aux rangs 0 et 1
Donc elle est vraie quel que soit le naturel k (ou n)
Initialisation :
Un = n est vraie aux rangs 0 et 1 (U0=0 et U1=1)
Hérédité :
Hypothèse de récurrence : Supposons Un=n vraie aux rangs k et k+1
c'est à dire Uk=k et Uk+1=k+1
Par hypothèse, Uk+2=2Uk+1 - Uk donc
Uk+2=2(k+1) - k = 2k + 2 - k = k + 2
Si Un=n est vraie aux rangs k et k+1 alors elle est vraie au rang k+2
Or elle est vraie aux rangs 0 et 1
Donc elle est vraie quel que soit le naturel k (ou n)
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
