j'ai à rendre pour la rentrée un DM de maths, j'ai déjà fait un exercice mais je coince sur quelques questions du deuxième.
En effet, l'exercice en question est le 76 p. 38 du manuel Barbazo de première.
Voici le sujet :

Je vous montre ma démarche pour ce que j'ai réussi :
Question 1 :
Dans la consigne, on sait que tous les rectangles Rn ont la même aire et que Ln correspond à sa longueur et ln à sa largeur.
On sait aussi que l'aire d'un rectangle = L * l
Donc Ln * ln.
On connait les dimensions de R0 : L0 = 5 et l0 = 1.
Donc,
Aire Rn = Ln * ln
Aire Rn = L0 * l0
Aire Rn = 5 * 1
Aire Rn = 5
Donc pour tout entier naturel n, Ln * ln = 5.
Question 2 :
On sait que Rn est toujours égal à 5. On sait aussi que Ln+1 est la moyenne des dimensions de Rn, c'est-à-dire de sa longueur et de sa largeur. Pour rappel la formule pour calculer une moyenne est :
Alors,
Je bloque pour justifier que
J'ai ensuite réussi pour la question 3 (je ne recopie pas puisqu'il s'agit juste de calculer, donc je ne pense pas m'être trompé).
Pour la question 4, je n'ai pas réussi à mettre la suite dans ma Ti 83 Premium CE qui m'indiquait à chaque fois une erreur mémoire, même si je la réinitialisait. J'ai donc tout calculé moi-même mais n'ai pas pu obtenir les résultats exacts à partir de R5 où la calculatrice ne m'a donné que des valeurs approchées à partir de là. Je mets ici les résultat en valeur approché que j'ai trouvé sur Excel afin de justifier la question suivante.
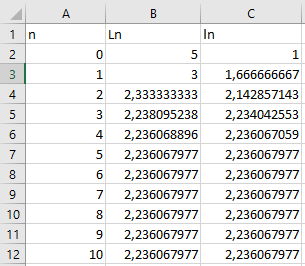
Question 5 :
Je conjecture donc que plus n tend vers l'infini, plus les longueur Ln et ln se rapprochent. Cela signifie donc que les dimensions de Rn deviennent de plus en plus proches et par conséquent, Rn se rapproche du carré.
Je ne sais pas si mes justifications sont assez claires et suffisantes et n'arrive pas à faire l'entièreté de la question 2. C'est pour cela que je vous appelle à l'aide

En vous remerciant par avance de m'aider !
P.S : je n'ai pas réussi à intégrer les fractions correctement

