Suite Géométrique

[Mlle.Ali]

Bonjours j'ai cet exercice à faire mais je ne comprend strictement pas grand chose.

Tout cancer débute par la production d'une cellule cancéreuse. Au cours du temps, cette cellule va produire un ensemble de cellules filles appelé tumeur.
On observe que le temps de doublement T d'une tumeur cancéreuse (c'est à dire le temps mis pour une tumeur donnée de doubler son nombre de cellules) est sensiblement constant pour un type de cancer donnée.
Ce temps dépend cependant du type de cancer.
Ce temps de doublement peut être évalué sur des cellules prélevées dans le tumeur et mises en culture.
Soit (Xn) la suite égale au nombre de cellules cancéreuses au bout de n périodes.
On pose X0 = 1
Actuellement, la plus petite tumeur cancéreuse détectable est constituée de 10^9 cellules ce qui correspond à peu près à une tumeur de masse égale à 1 gramme

1 Justifier que Xn=2^n

2 De source médicale, le temps nécessaire à la détection d'une tumeur issue d'une seule cellule cancéreuse est égal à 30 fois son temps de doublement, Justifier cette affirmation
Pour un cancer du sein T = 14 semaines

3 On part d'une cellule cancéreuse, Combien de temps doit-il s'écouler pour que celui ci soit détectable dans le cas d'un cancer du sein?

4 Après le traitement d'un cancer du sein, il est d'usage de surveiller la personne traitée sur une période de 5 ans. Sachant q'un traitement chirurgical peut laisser en résidu indétectable, une masse tumorale de 10^3 cellulesn expliquer l'origine du choix de 5 ans comme période de surveillance d'un cancer du sein après traitement chirurgical.

Pour la question 1 : D'après l'énoncé, la suite géométrique et par définition une suite géométrique si et seulement si il existe un réel q tel que Un+1 = U0 x q^n
Ici on aurait U0 = 1 au jour 1 et 2n correspond au doublement de la tumeur.

Pour la question 2 : La plus petite tumeur 10^9 cellules, on calcule 1+2^30?

Pour la question 3 : 14 semaine pour un temps de doublement, 5 ans?

Pour la question 4 : Comme un cancer du sein est détectable au bout de 5 ans, si celle si n'est pas réapparut au bout de 5 ans.

[Azertg13]

Ton exercice donne pas envie ...

[Ncdk]

Bonsoir qu'as-tu fait déjà ?

EDIT : J'ai mal lu, honte à moi.

Pour la première question, tu peux pourquoi pas faire une récurrence, car c'est plus ou moins ce que tu as remarqué, qu'on double à chaque période.

Pour la seconde question, oui c'est ça, du coup tu remarques que c'est plus grand que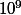 cellules, du coup ça colle bien

Pour la troisième question, je peux voir ta justification ? Mais en gros, c'est de savoir quand elle atteint au moins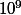 cellules, on te demande le temps nécessaire pour atteindre ce chiffre.