Suite Calculatrice
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Khyal
- Membre Naturel
- Messages: 53
- Enregistré le: 10 Jan 2013, 18:27
-
 par Khyal » 26 Mai 2013, 20:01
par Khyal » 26 Mai 2013, 20:01
"Soit (Un) = 2n+1/n²+1
1) A l'aide de la calculatrice, observez Un pour des grandes valeurs de n. Quelle conjecture peut-on faire sur la limite de Un?
2) Déterminez le plus petit entier n0 tel que 03)Déterminez le plus petit entier n0 tel que 0
Bonjour à tous, j'ai une calculatrice Casio 35+, je ne sais pas comment faire cet exercice, merci beaucoup de votre aide!
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 26 Mai 2013, 20:47
par XENSECP » 26 Mai 2013, 20:47
Alors tu as conjecturé la limite ?
-
Khyal
- Membre Naturel
- Messages: 53
- Enregistré le: 10 Jan 2013, 18:27
-
 par Khyal » 26 Mai 2013, 20:48
par Khyal » 26 Mai 2013, 20:48
Non, je ne comprends pas comment faire..
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 26 Mai 2013, 20:54
par XENSECP » 26 Mai 2013, 20:54
Tu prends des grandes valeurs de n et tu calcules pour en déduire (par intuition) la limite.
-
Khyal
- Membre Naturel
- Messages: 53
- Enregistré le: 10 Jan 2013, 18:27
-
 par Khyal » 26 Mai 2013, 21:12
par Khyal » 26 Mai 2013, 21:12
Avec quel programme de la calculatrice je fais ça?
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 26 Mai 2013, 21:24
par XENSECP » 26 Mai 2013, 21:24
Avec ta tête...
-
LaCoc6nl
- Membre Naturel
- Messages: 90
- Enregistré le: 29 Mar 2013, 19:06
-
 par LaCoc6nl » 26 Mai 2013, 21:42
par LaCoc6nl » 26 Mai 2013, 21:42
Khyal a écrit:Avec quel programme de la calculatrice je fais ça?
Le manuel de la Casio 35+ en page 27 explique comment programmer une suite et l'afficher. Lance-toi ...
-
Khyal
- Membre Naturel
- Messages: 53
- Enregistré le: 10 Jan 2013, 18:27
-
 par Khyal » 26 Mai 2013, 21:45
par Khyal » 26 Mai 2013, 21:45
Pour n = 100 Un = 0.02
pour n = 500, Un = 4
Pour n = 1 000, Un = 2
?
-
Liitou
- Messages: 8
- Enregistré le: 17 Mar 2013, 21:50
-
 par Liitou » 26 Mai 2013, 21:59
par Liitou » 26 Mai 2013, 21:59
T'as surement fait une erreur dans tes calculs parce que là tu as n²+1 au dénominateur! Donc plus la valeur de n augmente plus le quotient tend vers 0. D'où Un tend vers 0 lorsque n tend vers + l'infini
Khyal a écrit:Pour n = 100 Un = 0.02
pour n = 500, Un = 4
Pour n = 1 000, Un = 2
?
-
LaCoc6nl
- Membre Naturel
- Messages: 90
- Enregistré le: 29 Mar 2013, 19:06
-
 par LaCoc6nl » 26 Mai 2013, 22:09
par LaCoc6nl » 26 Mai 2013, 22:09
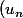)
définie par :
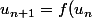)
est une fraction rationnelle dont la limite en +

est celle du quotient du terme de plus haut degré au numérateur et du terme de plus haut degré au dénominateur.
Une liste comportant 5 à 10 termes minimum permet de tracer un nuage de points plus représentatif de
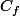
-
Khyal
- Membre Naturel
- Messages: 53
- Enregistré le: 10 Jan 2013, 18:27
-
 par Khyal » 27 Mai 2013, 17:34
par Khyal » 27 Mai 2013, 17:34
En refaisant mes calculs je trouve
Pour n =100, Un = 0.02
Pour n =1000, Un = 2.0*10^-3
Pour n =10 000, Un = 2.0+10^-4
Pour n =100 000, Un = 2.0*10^-5
Pour n =1 000 000, Un = 2.0*10^-6
Mais ça se rapproche de vers -infini..
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
