Bonjour !
J'ai un problème dans un exercice de spé maths :ptdr:
Voila l'exercice:
p entier naturel tel que 2^p - 1 premier
Soit Q= (2^p - 1 )*2^(p-1)
Il faut prouver que la somme entiers positif inf. ou ég. à son plus grand diviseur premier est égale à Q.
En d'autres terme égale à (2^p - 1 )*2^(p-1).
Si j'ai bien compris:
Si la décomposition en produit de facteurs premier de a c'est: a = b^c * d^e avec b<d Alors a = 1 + 2 + 3 + ... + d soit encore a = d(d+1)/2
C'est bien cela qu'il faut prouver non? :hein: Mais je n'arrive pas du tout à le démontrer ! On peut m'aider ?
Spé Maths: Arithmétique !!
2 messages
- Page 1 sur 1
si j'ai bien compris :
tu donnes p entier naturel tel que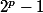 est premier
est premier
mais alors p est premier !
car sinon, pose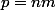 et et cherche la somme des n premiers termes de la suite géométrique de premier terme 1 et de raison
et et cherche la somme des n premiers termes de la suite géométrique de premier terme 1 et de raison 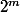
m}=\frac{2^{mn}-1}{2^m-1})
qui démontre la non primalité de
dans le cas où p est premier, tu tombes avec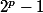 sur un classique nombre de Mersenne
sur un classique nombre de Mersenne
tu donnes p entier naturel tel que
mais alors p est premier !
car sinon, pose
qui démontre la non primalité de
dans le cas où p est premier, tu tombes avec
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
