Spé math : divisibilité et recurrence

[slavik]

Bonjour,
Je suis devant un problème de spé math.
Il faut montrer que pour tout naturel n, 7^(2n)+3 est divisible par 4.
Je sais utiliser la recurrence. Mais la je ne trouve pas comment faire.

[slavik]

J'arrive pas =(

[Sa Majesté]

Tu commences par l'initialisation et puis tu fais l'hérédité

[slavik]

Tu commences par l'initialisation et puis tu fais l'hérédité

Oui je sais utiliser la reccurrence mais j'arrive aps a le prouver par hérédité
J'arrive pas a factoriser par 7^(2n)+3

[Sa Majesté]

Pour l'hérédité tu supposes que est divisible par 4 et tu dois prouver que est divisible par 4

Comme il faut utiliser l'hypothèse, on peut avoir l'idée d'écrire
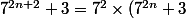A toi de compléter les ...

[slavik]

Pour l'hérédité tu supposes que est divisible par 4 et tu dois prouver que est divisible par 4

Comme il faut utiliser l'hypothèse, on peut avoir l'idée d'écrire
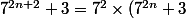A toi de compléter les ...

-144?


Et on peut utiliser cette methode pour tous les exercices par recurrence du genre?

[Sa Majesté]

-144?

Oui et là c'est dans la poche

Et on peut utiliser cette methode pour tous les exercices par recurrence du genre?

Probablement ...

[slavik]

Or 144=4*36
Donc 4 divise 7^(2(n+1))-3
Par consequent pour tout n, naturel, 4 divise 7^(2n)-3

[slavik]

MErci beaucoup, pff c'est dommage de bloquer la dessus pendant pas mal de temps, alors que c'est plutot facile :(

[Sa Majesté]

Or 144=4*36
Donc 4 divise 7^(2(n+1))-3
Par consequent pour tout n, naturel, 4 divise 7^(2n)-3

Oui sauf que c'est +3 et pas -3

[slavik]

Oui sauf que c'est +3 et pas -3

OUi désolé une erreur de frappe.

Et par example pour un énoncé du genre:
Prouver que 3^(2n)-2^n est divisible par 7
Comment on fait par recurrence?
J'arrive à
3^(2n+2)-2^(n+1)=3^2n*3²-2^n*2
Et je ne sais pas comment continuer.

[slavik]

C'est dans la meme serie d'exercices.

[Sa Majesté]

Il faut "forcer" la formule de l'hypothèse de récurrence

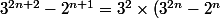[slavik]

Il faut "forcer" la formule de l'hypothèse de récurrence

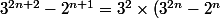+(2^n)(3²-2)
C'es ca?

Or d'apres l'hypothese de debut 3^(2n)-2^n est divisible par 7
Pour n=1 on a 3^(2n)-2^n=(3²-2) ainsi 7 divise (3²-2)

Donc c'est vrais pour tout rang n.


Mais est-ce la seule difiicultée à laquelle on pourra etre confronté dans la recurrence à notre niveau? Où il y a d'autres methodes que de "forcer" la formule.

[Sa Majesté]

+(2^n)(3²-2)
C'es ca?

Oui c'est ça

Or d'apres l'hypothese de debut 3^(2n)-2^n est divisible par 7
Pour n=1 on a 3^(2n)-2^n=(3²-2) ainsi 7 divise (3²-2)

Je ne vois pas pourquoi tu parles de n=1
Il faut dire que 2^n(3²-2)=7.2^n est divisible par 7

Mais est-ce la seule difiicultée à laquelle on pourra etre confronté dans la recurrence à notre niveau? Où il y a d'autres methodes que de "forcer" la formule.

En sachant ça tu dois pouvoir te sortir de la plupart des situations

[slavik]

Oui c'est ça

Je ne vois pas pourquoi tu parles de n=1
Il faut dire que 2^n(3²-2)=7.2^n est divisible par 7

En sachant ça tu dois pouvoir te sortir de la plupart des situations

Merci vous m'avez vraiment aidé!!!
=)