--- Spé math Divisibilité ---
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 30 Sep 2006, 15:56
par theluckyluke » 30 Sep 2006, 15:56
Bonjour tout le monde,
en fait je bloque sur un exercice de Spé Math, j'ai du mal à comprendre ce chapitre. Quelqu'un pourrait-il m'aider pour les deux exos qui suivent?
I)
On désigne par n et a deux entiers naturels. Démontrer que si a divise 5n+31 et a divise 3n+12, alors a divise 33. Déterminer toutes les valeurs possibles pour les entiers a et n.
II)
Déterminer les entiers naturels n tels que le quotient

soit un entier.
Merci d'avance pour vos réponses!
-
webnet
- Membre Relatif
- Messages: 189
- Enregistré le: 08 Sep 2006, 18:09
-
 par webnet » 30 Sep 2006, 16:08
par webnet » 30 Sep 2006, 16:08
Salut,
Pour le 1) il y a une propriété, appliquée à ton exemple qui dit que si a divise 5n+31 et a divise 3n+12 alors a divise toute combinaison linéaire de u(5n+31)+ v(3n+12). Tu détermines u et v pour que les n s' annulent
Pour 2) tu peux essayer une méthode similaire, ou bien dire que le numérateur est toujours inférieur ou égal au dénominateur, tu cherche n ( sous forme d' inégalité ) et tu vérifies si ils sont solution ( en n oubliant pas q ils sont naturels
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 30 Sep 2006, 16:23
par theluckyluke » 30 Sep 2006, 16:23
en fait je trouve avec ta manière :
 +31k+12k' = a)
avec k et k' entier
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 01 Oct 2006, 16:42
par theluckyluke » 01 Oct 2006, 16:42
je suis bloqué là, personne pour m'aider?
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 01 Oct 2006, 17:07
par BancH » 01 Oct 2006, 17:07
theluckyluke a écrit:II)
Déterminer les entiers naturels n tels que le quotient

soit un entier.
Tu peux utiliser une méthode bidon:
Lorsque

tend vers


tend vers

donc






-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 01 Oct 2006, 17:14
par BancH » 01 Oct 2006, 17:14
Je n'avais pas vu que webnet avait déjà donné la réponse...
webnet a écrit:Pour 2) tu peux essayer une méthode similaire, ou bien dire que le numérateur est toujours inférieur ou égal au dénominateur, tu cherche n ( sous forme d' inégalité ) et tu vérifies si ils sont solution ( en n oubliant pas q ils sont naturels
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 01 Oct 2006, 18:05
par theluckyluke » 01 Oct 2006, 18:05
BancH a écrit:Je n'avais pas vu que webnet avait déjà donné la réponse...
merci BancH!!
quelqu'un peut m'éclairer pour le I) ???
EDIT: c'est bon j'ai compris
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 01 Oct 2006, 18:09
par theluckyluke » 01 Oct 2006, 18:09
Pour le 1) il y a une propriété, appliquée à ton exemple qui dit que si a divise 5n+31 et a divise 3n+12 alors a divise toute combinaison linéaire de k(5n+31)+ k'(3n+12). Tu détermines u et v pour que les n s' annulent
Donc k est un multiple de 3 et k' est un multiple de 5 tel que :
5nk = 3nk'
5nk - 3nk' = 0
n (5k - 3k') = 0
n(5k+3k') +31k+12k' = a
avec k et k' entier
donc 31k+12k' = a
J'avoue je ne sais pas trop comment poursuivre...
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 01 Oct 2006, 18:23
par BancH » 01 Oct 2006, 18:23
theluckyluke a écrit:I)
On désigne par n et a deux entiers naturels. Démontrer que si a divise 5n+31 et a divise 3n+12, alors a divise 33. Déterminer toutes les valeurs possibles pour les entiers a et n.
Tu devrais trouver:
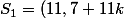)
et
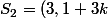)
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 01 Oct 2006, 18:40
par theluckyluke » 01 Oct 2006, 18:40
BancH a écrit:Tu devrais trouver:
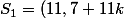)
et
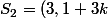)
comment tu trouves cela?
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 01 Oct 2006, 19:46
par Quidam » 01 Oct 2006, 19:46
theluckyluke a écrit:en fait je trouve avec ta manière :
 +31k+12k' = a)
avec k et k' entier
theluckyluke a écrit:Donc k est un multiple de 3 et k' est un multiple de 5 tel que :
5nk = 3nk'
5nk - 3nk' = 0
n (5k - 3k') = 0
Non. k peut être n'importe quoi et k' aussi. Il faut dire SI je choisis k comme multiple de 3 :
k=3m
Pour annuler le coefficient de n (qui est 5k+3k') il suffirait que
5k+3k'=0
soit
5*(3m)+3k'=0
soit 3*(5m+k')=0
Donc il suffit de choisir k'=-5m mon équation peut s'écrire avec ces deux valeurs particulières de k et k' (j'en ai le droit puisque cela est vrai quel que soient k et k') :
 +31k+12k' = a)
) +31*3m+12*(-5m) = a)
m = a)
m = a)
CQFD
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 02 Oct 2006, 16:10
par theluckyluke » 02 Oct 2006, 16:10
OK merci Quidam, c'est déjà plus clair... je vais essayer de le refaire pour voir
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
