Sin(x)-x^2

par **mok9093** » 01 Nov 2018, 14:42

Salut,
Soit f la fonction définie par: f(x)=sin(x)-

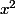
1) Montrer que: (∃α∈]

[ : f(α)=0
2)En déduire que l'équation cos(x)-2x=0 admet une solution dans IR
Cette solution est-elle unique? Justifier

pour la première question j'ai essayé le théorème des valeurs intérmediaires et j'ai trouvé l'unicité mais pas l'existence comme ils ont dit.

et pour la deuxieme question je ne sais quoi faire. Avez vous une idéé?

Cordialement,

par **jlb** » 01 Nov 2018, 14:47

Oui!

par **jlb** » 01 Nov 2018, 14:48

Sinon, pour être plus constructif, tu donnes ton explication pour la question 1) pour commencer!

par **mok9093** » 01 Nov 2018, 14:57

jlb a écrit:::d Oui!

j'ai utilisé le TVI (la continuité et 0 appartient à l'image de l'intervalle)

par **hdci** » 01 Nov 2018, 15:01

Et bien le TVI te donne l'existence, mais pas l'unicité !
Comment as-tu trouvé l'unicité ?

par **mok9093** » 01 Nov 2018, 15:03

hdci a écrit:Et bien le TVI te donne l'existence, mais pas l'unicité !
Comment as-tu trouvé l'unicité ?

quand je voulais étudier la monotonie de f pour faire l'image j'ai trouvé que f est strictement croissante

par **mok9093** » 01 Nov 2018, 15:05

strict décroissante plutot

par **jlb** » 01 Nov 2018, 15:09

Ok, bon après, tu calcules f(0) et la fonction étant continue et dérivable sur [0; pi/2], au moins une tangente à la courbe doit être parallèle à l'axe de abscisses: la dérivée de f doit donc s'annuler sur l'intervalle.

remarque: (1) sur l'intervalle [pi/4,pi/2], f est strictement décroissante, cela te donne l'unicité.
(2) as-tu dérivé f? Et étudie le comportement de f' ( rappel: -1 <= sinx<= 1 pour tout x réel)

par **mok9093** » 01 Nov 2018, 15:13

on peut dire que Cf admet une tangente que si f(0)=f(pi/2) dans ce cas ils sont différents

je n'ai pas compris la 2eme remarque

par **jlb** » 01 Nov 2018, 15:18

Tu as trouvé alpha dans la première question tel que f(alpha) = 0 et f(0) =….

Tu n'as pas appris à dériver?

par **mok9093** » 01 Nov 2018, 15:25

jlb a écrit:Tu as trouvé alpha dans la première question tel que f(alpha) = 0 et f(0) =….

Tu n'as pas appris à dériver?

oui donc le 0 est unique comme on a dit tq f(0)=0 j'ai dérvié f j'ai obtenu l'équation dans la deuxieme question quelle est la prochaine étape à faire

par **mok9093** » 01 Nov 2018, 15:55

par **jlb** » 01 Nov 2018, 15:58

Tu dérives encore une fois et tu cherches le signe.

par **mok9093** » 01 Nov 2018, 16:25

j'ai dérivé cos(x)-2x la dérivée est positive donc croissante mais je sais pas ou s'annule cos(x)-2x

par **mok9093** » 01 Nov 2018, 16:47

par **mok9093** » 01 Nov 2018, 17:10

par **Miatonu** » 01 Nov 2018, 17:27

bon courage mdr

par **pascal16** » 01 Nov 2018, 17:56

sans aucun calcul, juste sur de considérations d'énoncés
f(pi/4)>0
f(pi/2)<0
f strictement décroissante
f continue
le tvi dit il existe alpha entre pi/4 et pi/2 tel que f(alpha)=0

par **pascal16** » 01 Nov 2018, 18:00

pour la 2
si g est la fonction dont on cherche un zéro
g(-10) et g(10) ont des signes opposés, g s'annule entre -10 et 10, mais par forcément une seule fois

fais un "zoom" sur g entre pi/4 et pi/2
la question 1 doit te permettre de faire le tableau de variations de g

par **mok9093** » 01 Nov 2018, 18:12

ca va nous servir à quoi le tableau de variations?

Sin(x)-x^2

sin(x)-x^2

Re: sin(x)-x^2

Re: sin(x)-x^2

Re: sin(x)-x^2

Re: sin(x)-x^2

Re: sin(x)-x^2

Re: sin(x)-x^2

Re: sin(x)-x^2

Re: sin(x)-x^2

Re: sin(x)-x^2

Re: sin(x)-x^2

Re: sin(x)-x^2

Re: sin(x)-x^2

Re: sin(x)-x^2

Re: sin(x)-x^2

Re: sin(x)-x^2

Re: sin(x)-x^2

Re: sin(x)-x^2

Re: sin(x)-x^2

Re: sin(x)-x^2

Qui est en ligne