Simplification et factorisation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 03 Avr 2012, 15:15
par Dante0 » 03 Avr 2012, 15:15
Bonjour,
Comment simplifer les expressions suivantes :
1)

2)

Pour la première je propose :

Quid de la seconde ?
Ensuite je dois factoriser :
^5 +5x^3(x+1)^4)
Merci

-
Black Jack
 par Black Jack » 03 Avr 2012, 15:35
par Black Jack » 03 Avr 2012, 15:35
Dante0 a écrit:Bonjour,
Comment simplifer les expressions suivantes :
1)

2)

Pour la première je propose :

Quid de la seconde ?
Ensuite je dois factoriser :
^5 +5x^3(x+1)^4)
Merci

Attention aux valeurs interdites.
La relation (1) est équivalente à (x+2) ... à la condition que x soit différent de 2
*****
Pour la (2)
- Rechercher les valeurs interdites de x ...
- Se rappeler que diviser par une fraction est équivalent à multiplier par l'inverse de la fraction.
- factoriser le numérateur et le dénominateur obtenus.
- simplifier.
:zen:
-
antonyme
- Membre Relatif
- Messages: 435
- Enregistré le: 28 Mar 2012, 16:07
-
 par antonyme » 03 Avr 2012, 15:45
par antonyme » 03 Avr 2012, 15:45
Dante0 a écrit:Ensuite je dois factoriser :
^5 +5x^3(x+1)^4)
Tu peut isoler
^4)
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 03 Avr 2012, 15:59
par Dante0 » 03 Avr 2012, 15:59
Hum je trouve :

-
Azz
- Membre Naturel
- Messages: 37
- Enregistré le: 08 Oct 2010, 11:04
-
 par Azz » 03 Avr 2012, 18:39
par Azz » 03 Avr 2012, 18:39
Salut tu connais les divisions euclidiennes? Parce que je pense que ce tu viens de faire n'est pas une factorisation !
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 03 Avr 2012, 19:32
par Dante0 » 03 Avr 2012, 19:32
Azz a écrit:Salut tu connais les divisions euclidiennes? Parce que je pense que ce tu viens de faire n'est pas une factorisation !
Non je parlais de la 2) ou je dois simplifier.
-
Azz
- Membre Naturel
- Messages: 37
- Enregistré le: 08 Oct 2010, 11:04
-
 par Azz » 03 Avr 2012, 19:48
par Azz » 03 Avr 2012, 19:48
Si tu divise par X²(x+1)^4 . Tu trouves 3(x+1)+5x..
-
antonyme
- Membre Relatif
- Messages: 435
- Enregistré le: 28 Mar 2012, 16:07
-
 par antonyme » 03 Avr 2012, 20:12
par antonyme » 03 Avr 2012, 20:12
Dante0 a écrit:Hum je trouve :

Tu peux encore enlever 2x. Et puis, même si cela dépend de ce que tu veux faire avec, la plupart du temps il est plus pratique de garder le dénominateur sous la forme factorisé.
Enfin, comme l'a dit Black Jack, n'oublis pas de lister les valeurs interdites.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 03 Avr 2012, 20:19
par Dante0 » 03 Avr 2012, 20:19
antonyme a écrit:Tu peux encore enlever 2x. Et puis, même si cela dépend de ce que tu veux faire avec, la plupart du temps il est plus pratique de garder le dénominateur sous la forme factorisé.
Enfin, comme l'a dit Black Jack, n'oublis pas de lister les valeurs interdites.
(x+4)})
Ok

Je peux passer à la factorisation maintenant.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 03 Avr 2012, 20:24
par Dante0 » 03 Avr 2012, 20:24
antonyme a écrit:Tu peut isoler
^4)
Je trouve :
^4(8x+3))
je peux aller plus loin ?
-
antonyme
- Membre Relatif
- Messages: 435
- Enregistré le: 28 Mar 2012, 16:07
-
 par antonyme » 03 Avr 2012, 20:56
par antonyme » 03 Avr 2012, 20:56
Dante0 a écrit:Je trouve :
^4(8x+3))
je peux aller plus loin ?
C'est exactement ça et non je ne pense pas que tu puisse allez plus loin mais c'est déjà pas mal non :zen:
Dante0 a écrit:(x+4)})
Ok

Je peux passer à la factorisation maintenant.
C'est ça, mais n'oublie pas de dire que cette fraction est égale à ta fraction de départ seulement si x est différent de -4, -1, 0 et 1
Bravo! :++:
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 04 Avr 2012, 08:38
par Dante0 » 04 Avr 2012, 08:38
antonyme a écrit:C'est exactement ça et non je ne pense pas que tu puisse allez plus loin mais c'est déjà pas mal non :zen:
C'est ça, mais n'oublie pas de dire que cette fraction est égale à ta fraction de départ seulement si x est différent de -4, -1, 0 et 1
Bravo! :++:
Okay merci !

-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 05 Avr 2012, 09:43
par Dante0 » 05 Avr 2012, 09:43
Bonjour,
Vous sauriez répondre à cette question :
let
 = (x-\sqrt{x})^3)
Find f(4) and f'(4)
Approximate the change in the function value if x increases with 0.01 (from x = 4).
Give the relationship between this approximation and f '(4).
c. Find the equation of the tangent at the graph of f for x = 4.
Je trouve
 = 8)
et
 = 9)
mais je bloque sur la question suivante.
-
Black Jack
 par Black Jack » 05 Avr 2012, 10:47
par Black Jack » 05 Avr 2012, 10:47
Dante0 a écrit:Bonjour,
Vous sauriez répondre à cette question :
let
 = (x-\sqrt{x})^3)
Find f(4) and f'(4)
Approximate the change in the function value if x increases with 0.01 (from x = 4).
Give the relationship between this approximation and f '(4).
c. Find the equation of the tangent at the graph of f for x = 4.
Je trouve
 = 8)
et
 = 9)
mais je bloque sur la question suivante.
On te demande probablement une approximation affine.
 \simeq f(xo) + f'(xo).h)
... si h est petit.
Et donc :
 \simeq f(4) + 0,01.f'(4))
f(4,01) = ...
...
:zen:
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 05 Avr 2012, 10:57
par Dante0 » 05 Avr 2012, 10:57
Black Jack a écrit:On te demande probablement une approximation affine.
 \simeq f(xo) + f'(xo).h)
... si h est petit.
Et donc :
 \simeq f(4) + 0,01.f'(4))
f(4,01) = ...
...
:zen:
C'est quoi déja ? :/
Ca remonte à la 1ere S...
-
antonyme
- Membre Relatif
- Messages: 435
- Enregistré le: 28 Mar 2012, 16:07
-
 par antonyme » 05 Avr 2012, 11:18
par antonyme » 05 Avr 2012, 11:18
Dante0 a écrit:C'est quoi déja ? :/
Ca remonte à la 1ere S...
L'équation de la tangente en un point

est
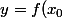+f'(x_0)(x - x_0))
et si tu te déplace un tout petit peu sur l'axe des abscisses (de h) l'erreur sera faible. On peu alors donné ce qu'on appelle l'approximation affine de l'image de
)
en utilisant l'équation de la tangente. C'est à dire
 \approx f(x_0)+f'(x_0)(x_0+h-x_0))
ou encore
 \approx f(x_0)+f'(x_0).h)
Je sais pas si je suis bien clair :hum:
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 05 Avr 2012, 15:41
par Dante0 » 05 Avr 2012, 15:41
antonyme a écrit:L'équation de la tangente en un point

est
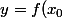+f'(x_0)(x - x_0))
et si tu te déplace un tout petit peu sur l'axe des abscisses (de h) l'erreur sera faible. On peu alors donné ce qu'on appelle l'approximation affine de l'image de
)
en utilisant l'équation de la tangente. C'est à dire
 \approx f(x_0)+f'(x_0)(x_0+h-x_0))
ou encore
 \approx f(x_0)+f'(x_0).h)
Je sais pas si je suis bien clair :hum:
Euh oui, du coup c'est juste une formule à appliquer ?
-
antonyme
- Membre Relatif
- Messages: 435
- Enregistré le: 28 Mar 2012, 16:07
-
 par antonyme » 05 Avr 2012, 16:05
par antonyme » 05 Avr 2012, 16:05
Dante0 a écrit:Euh oui, du coup c'est juste une formule à appliquer ?
Tu peux tout simplement apprendre la formule mais le mieux c'est de comprendre comment on arrive à cette formule :lol3:
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 05 Avr 2012, 16:41
par Dante0 » 05 Avr 2012, 16:41
antonyme a écrit:Tu peux tout simplement apprendre la formule mais le mieux c'est de comprendre comment on arrive à cette formule :lol3:
La réponse ce serait donc
 = 8,009)
?
-
antonyme
- Membre Relatif
- Messages: 435
- Enregistré le: 28 Mar 2012, 16:07
-
 par antonyme » 05 Avr 2012, 16:50
par antonyme » 05 Avr 2012, 16:50
Dante0 a écrit:La réponse ce serait donc
 = 8,009)
?
Ta réponse n'est pas fausse mais la question concernait
)
:lol3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 158 invités
je peux aller plus loin ?
Ok
et
mais je bloque sur la question suivante.
est
et si tu te déplace un tout petit peu sur l'axe des abscisses (de h) l'erreur sera faible. On peu alors donné ce qu'on appelle l'approximation affine de l'image de
en utilisant l'équation de la tangente. C'est à dire
ou encore
 \approx f(x_0)+f'(x_0).h)