Seconde fonction démonstration

[MoumoucheO]

Bonjour,

J'ai un DM de maths et je bloque sur une question que je ne comprend pas trop et que j'ai beau chercher je ne trouve pas la solution j'espère que vous pourrez m'aider, merci d'avance.

Soit la fonction f définie sur R par f(x) = x²-8x+7

La question : Pour tout x appartient R démontrer que f(x) est plus grand ou égal à -9. En déduire que f admet -9 comme minimum. Justifer.

Précedement j'ai du montrer que f(x) = (x-4)²-9
en déduire sa formule factorisée et résoudre f(racinede3), f(x)=7, f(x)=-9 et f(4)

Merci pour votre aide.

[mcar0nd]

Salut, si ta fonction f admet -9 comme minimum, ça veut dire . Il faut donc que tu prouve ça.

[MoumoucheO]

Mais comment savoir que -9 est le minimum?

[mcar0nd]

Mais comment savoir que -9 est le minimum?

Dans ta question, on te demande de prouver que c'est le minimum. Pour l'instant, tu ne peux pas le trouver directement si on ne te le donne pas.
Il faut donc que tu résolve l'inéquation .

[MoumoucheO]

Je n'arrive pas a résoudre cette inéquation j'arrive a x²plus grand ou égal a -16+8x ...

[mcar0nd]

Je n'arrive pas a résoudre cette inéquation j'arrive a x²plus grand ou égal a -16+8x ...

L'inéquation c'est d'après la question précédente.

[MoumoucheO]

Oui mais je n'arrive pas ensuite cela fait : (x-4)²-9 plus grand ou égal a -9
(x-4)² plus grand ou égal a 0
(x-4)(x-4) plus grand ou égal a 0
x²-8x+16 plus grand ou égal a 0
et après je suis bloqué..

[mcar0nd]

Oui mais je n'arrive pas ensuite cela fait : (x-4)²-9 plus grand ou égal a -9
(x-4)² plus grand ou égal a 0
(x-4)(x-4) plus grand ou égal a 0
x²-8x+16 plus grand ou égal a 0
et après je suis bloqué..

En fait, quand tu es arrivé à la deuxième ligne, c'est presque terminé. Quel est le signe d'un carré?

[ampholyte]

Bonjour,

Par définition : un carré est toujours positif donc
(x - 4)² >= 0
=)

[MoumoucheO]

Un carré est toujours positif?

[mcar0nd]

Un carré est toujours positif?

Attention, un carré est toujours positif ou nul.
Donc ton inéquation est vérifiée pour tous x appartenant à R.

[MoumoucheO]

Donc ici x est compris entre 4 et +l'infini c'est ça?

[mcar0nd]

Donc ici x est compris entre 4 et +l'infini c'est ça?

Non, la fonction que tu as est définie sur R. Ton inéquation est vérifiée pour les x appartenant à R; ce qui veut dire que ta fonction est toujours supérieure ou égale à -9, jamais elle prend des valeurs inférieures à -9.

[MoumoucheO]

Ah oui je crois commencé a comprendre, mais comment je peut rédiger ça? :o

[mcar0nd]

Ah oui je crois commencé a comprendre, mais comment je peut rédiger ça?

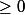
Bah premièrement, tu résous ton équation, tu arrive à , donc là tu dis, un carré est toujours donc l'inéquation est vraie pour tous x appartenant à R.
Et ensuite, est ce que tu peux en déduire que -9 est le minimum?

[MoumoucheO]

D'accord! Et bien oui parce que pour tout x inférieur a -9 l'inéquation n'est pas vrai c'est ça?

[mcar0nd]

D'accord! Et bien oui parce que pour tout x inférieur a -9 l'inéquation n'est pas vrai c'est ça?

Alors oui c'est ça mais c'est mal dit. Il faut que tu dise que pour réel x, f(x) est supérieur ou égal à -9 donc -9 est le minimum de ta fonction.

[MoumoucheO]

d'accord! Merci beaucoup j'y vois plus clair!!!

D'autre part, j'ai résolut 2 équations et je ne suis pas sure d'avoir les bonnes réponses,

1) (2x+1)²-(x-2)²=0 j'ai mis que les solutions étaient 1/3 et -1

2) (2x-1)/(x+3)=1 valeur interdite : -3 et solution x=4

[mcar0nd]

d'accord! Merci beaucoup j'y vois plus clair!!!

D'autre part, j'ai résolut 2 équations et je ne suis pas sure d'avoir les bonnes réponses,

1) (2x+1)²-(x-2)²=0 j'ai mis que les solutions étaient 1/3 et -1

2) (2x-1)/(x+3)=1 valeur interdite : -3 et solution x=4

Alors, tout n'est pas juste.
On va commencer par la première équation, tu as factorisé après avoir remarqué l'identité remarquable, mas -1 n'est pas une solution. Montre moi ce que tu trouves comme factorisation stp.

[MoumoucheO]

Je trouve ((2x+1)+(x-2)) * ((2x+1)-(x-2))=0
(3x-1)*(3x+3)=0
on a un produit de facteur nul donc l'un des facteur est nul

3x-1=0 x=1/3
ou
3x+3=0 x=-1