Résoudre dans R inéquations

[alexialj]

Bonjour j’ai un devoir à rendre pour demain et je bloque sur un exercice qui est de résoudre dans R les inéquations suivantes en détaillant les calculs :

A) -6x*2 + 4x + 2 inférieur à 0
B) 3 x sur 1-x inférieur ou égal à 0
C) -4x*2 + 4x - 1 sur x-3 supérieur a 0
D) 16-x*2 sur x*2-x-6 inférieur ou égal à 0

Pourriez vous m’aider ?

[Lostounet]

Salut
Pour les quatre c'est exactement la même méthode...
Aucune astuce ni rien: tu dois factoriser le numérateur (en utilisant par exemple le discriminant delta) puis factoriser le dénominateur.
Puis faire un tableau de signes...

[alexialj]

Allez pour la 1 j’ai trouver que delta était égal à 24 et il y’a deux solutions 2+racine de 6 sur 6 et 2- racine de 6 sur 6
Ensuite qu’est ce que je fais ? Merci beaucoup

[Lostounet]

Le delta est faux...

[alexialj]

mince ça fait 64 excusez moi avec pour solutions 1 et -1/3 donc la j’ai réussis mais comme la deuxième est pas de forme ax*2+ bx+ c je sais pas comment faire

[Lostounet]

Mais attend c'est pas fini.

Tu dois factoriser et étudier le signe du produit de facteurs au 1.

[alexialj]

J’en ai archi marre je comprend rien

[Lostounet]

J’en ai archi marre je comprend rien

Bon...
Il faut inspirer et expirer déjà ....

Il faut se concentrer sur un exercice puis sur l'autre.
On arrivera pas à faire les deux si tu as du mal partout, non?

Donc on commence par lequel? Celui-ci est très simple à faire une fois que tu comprends le 1 et le 2.

Donc pour commencer...je te pose une question qui n'est pas liée à l'exo.
Peux-tu me donner le signe des calculs suivants ? (Positif ou négatif?) Et comment tu sais?

A = (-2)×(3)

B=(-100)/(-3)

[alexialj]

A décroissant + au -
B croissant - au +

[alexialj]

Merci beaucoup de m’accorder votre temps

[Lostounet]

A décroissant + au -
B croissant - au +

Attention. A et B sont deux nombres.. ils ne décroissent pas ni ne croissent...

A et B sont deux nombres et je te demande uniquement de me dire si A est positif ou négatif.
Et de me dire si B est positif ou négatif.

Et pourquoi

[alexialj]

A est négatif car ça fait -6
Et b est positif car - par - ça fait +

[Lostounet]

A est négatif car ça fait -6
Et b est positif car - par - ça fait +

Oui: A est négatif car c'est le produit d'un nombre positif et d'un nombre négatif.

B est positif car on divise un nombre négatif par un autre.

Maintenant peux-tu me dire pour le nombre suivant, s'il est positif ou négatif mais SANS le calculer:

73937 - 82728 + 2 ?

Tu vas te rendre compte que c'est difficile!
La moralité de l'histoire est que quand on a une multiplication ou une division il est plus facile de dire si un nombre est négatif ou positif.

Quand on a une addition/soustraction c'est pas évident... es-tu d'accord?

[alexialj]

Oui je suis totalement d’accord et ce nombre sera négatif

[alexialj]

J’ai réussis la A silvouplait passons à la B j’aimerais ne pas peter un plomb d’ici ce soir xD

[Lostounet]

Donc maintenant, on va partir de ce constat très simple pour résoudre ton exercice.

Prenons le premier:

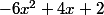est un polynôme. Cela signifie que pour chaque x que je choisis, j'ai un nombre différent. Par exemple pour x=0, je trouve 2.
Pour x=1, je trouve -6+4+2=0

Selon la valeur de x que je choisis, le nombre trouvé est différent. On s'intéresse à savoir, pour quels x que je choisis au départ, est-ce que le polynôme est négatif. Cela est pareil que de dire, en termes savants, résoudre l'inéquation
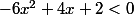(plus petit que 0 veut dire négatif).

Maintenant si tu fais le lien avec ce qu'on a dit avant, on s'est mis d'accord que pour voir si un nombre est négatif est positif, il est plus facile qu'il soit écrit sous la forme de multiplication de nombres dont on connait le signe non? (Comme le nombre A).

Ici, malheureusement on a affaire à une somme pas à une multiplication. Donc ce qu'on fait, c'est transformer cette somme:
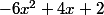en multiplication (comme tu as dû apprendre à faire en cours en utilisant delta etc...).

Maintenant qu'on a obtenu une forme plus jolie, il suffit de regarder le signe de chaque élément de cette multiplication.

(-6) est négatif
(x-1) est négatif lorsque x<1 (tu es d'accord?)
(x+1/3) est négatif lorsque x+1/3<0 donc x<-1/3


Donc en fait quand je choisis x plus petit que -1/3 et plus petit que 1, je fais le produit de (-6) *(x-1)*(x+1/3) qui sont trois nombres négatifs dans ce cas.

- par - par - donne -... donc ces valeurs de x rendent le polynôme négatif.

Bonjour j’ai un devoir à rendre pour demain et je bloque sur un exercice qui est de résoudre dans R les inéquations suivantes en détaillant les calculs :

A) -6x*2 + 4x + 2 inférieur à 0
B) 3 x sur 1-x inférieur ou égal à 0
C) -4x*2 + 4x - 1 sur x-3 supérieur a 0
D) 16-x*2 sur x*2-x-6 inférieur ou égal à 0

Pourriez vous m’aider ?

[Lostounet]

J’ai réussis la A silvouplait passons à la B j’aimerais ne pas peter un plomb d’ici ce soir xD

Ok donc je viens de taper tout ca pour rien.. tu veux juste finir tes devoirs sans comprendre.
Mes parents m'avaient prévenu de pas faire prof et ils avaient raison.

[alexialj]

Je trouve vos explications très nettes et précises et je vous en remercie et non j’en veux pas le faire sans comprendre c’est juste que si je commence à m’attarder j’y suis encore à 4h du matin ..

[Lostounet]

Alors si tu as vraiment compris les 4 sont exactement pareils.

Donc mets toutes les réponses et on te dira si juste ou pas.

[alexialj]

Non la 2 eme n’est pas pas pareille