Si.
Elle est même plus simple car il n'y a rien à factoriser.
Résoudre dans R inéquations
33 messages
- Page 2 sur 2 - 1, 2
Re: Résoudre dans R inéquations
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Résoudre dans R inéquations
On n'a pas besoin de delta!
Si tu as lu ce que je t'ai dit je t'ai expliqué exactement ce que tu dois faire: regarder le signe de chaque terme
Si tu as lu ce que je t'ai dit je t'ai expliqué exactement ce que tu dois faire: regarder le signe de chaque terme
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Résoudre dans R inéquations
J’abandonne je rend copie blanche j’y suis depuis 16h ça me monte à la tête
Re: Résoudre dans R inéquations
Non mais attends...
Qu'attends-tu exactement de moi?
J'ai essayé de t'expliquer, tu ne veux pas car pas le temps.
Je te dis ok, montre moi tes réponses que je les corrige... tu ne veux/sais pas.
Donc que faut-il que je fasse?
Que je rende une copie à ta place?..
Pourquoi tu t'y prends si tard en sachant que tu as autant de mal
Qu'attends-tu exactement de moi?
J'ai essayé de t'expliquer, tu ne veux pas car pas le temps.
Je te dis ok, montre moi tes réponses que je les corrige... tu ne veux/sais pas.
Donc que faut-il que je fasse?
Que je rende une copie à ta place?..
Pourquoi tu t'y prends si tard en sachant que tu as autant de mal
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Résoudre dans R inéquations
Mais je comprend pass je comprend rien j’en ai ras le’ bol des maths ça me pourri la vie depuis ma naissances !!
Re: Résoudre dans R inéquations
Expliquez moi plutôt pour le sujet « QCMre) je pense que je vais plus comprendre svp
Re: Résoudre dans R inéquations
Est-ce que c'est noté?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Résoudre dans R inéquations
Malheureusement oui si j’ai pas au moins 10 à ce devoir je ne dépasserais pas les 5 de moyenne en maths ..
Re: Résoudre dans R inéquations
Et si tu as une bonne note?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Résoudre dans R inéquations
Bon...
Ce n'est pas un service que je te rends mais je ne veux pas que tu ais 5 de moyenne.
ça me fait de la peine.
Je vais faire quelques exercices, à condition que tu t'y prennes à l'avance la prochaine fois. Et aussi à condition que tu fasses un effort pour comprendre.. sinon ça sert vraiment à rien franchement.
A toi de rédiger proprement...
A) On factorise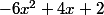 , delta = 64, on a deux solutions x = ...= 1, x = ... = -1/3, donc on a la factorisation
, delta = 64, on a deux solutions x = ...= 1, x = ... = -1/3, donc on a la factorisation (x - 1) <= 0)
Donc le trinome de degré 2,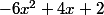 est toujours du signe de a = -6, donc négatif sauf entre les deux racines, donc sauf sur l'intervalle [-1/3 ; 1] sur lequel il est positif.
est toujours du signe de a = -6, donc négatif sauf entre les deux racines, donc sauf sur l'intervalle [-1/3 ; 1] sur lequel il est positif.
En conclusion, l'ensemble des solutions est :
B) 3x/(1 - x) < 0
Cette inéquation est définie pour tout x différent de 1.
On a 3x < 0 pour x < 0
et (1 - x)< 0 pour x > 1
Donc (tableau de signes) l'ensemble des solutions est:
C) Factorisons: -4x*2 + 4x - 1 . On constate une identité remarquable:
L
 = -4(x - 1/2)^2) donc le numérateur est toujours négatif. L'inéquation n'est pas définie en x = 3.
donc le numérateur est toujours négatif. L'inéquation n'est pas définie en x = 3.
On étudie le signe du dénominateur, (x - 3) > 0 lorsque x>3. et (x - 3) < 0 lorsque x < 3
donc l'ensemble des solutions est
D) Factorisons le numérateur, on a une identité remarquable (16 - x^2) = (4 - x)(4 + x)
Par ailleurs, factorisons x^2-x-6 a pour discriminant delta = 25, donc deux solutions etc... donc la factorisation est = (x + 2)(x - 3))
L'inéquation n'est donc pas définie en x = -2 et x = 3
On a donc le tableau de signes suivant (tu traces le tableau avec les nombres 4, -4, -2 et 3 rangés par ordre et tu marques les signes de chaque terme. Regarde sur le net comment on présente le tableau.
On conclut que l'ensemble des solutions est
Ce n'est pas un service que je te rends mais je ne veux pas que tu ais 5 de moyenne.
ça me fait de la peine.
Je vais faire quelques exercices, à condition que tu t'y prennes à l'avance la prochaine fois. Et aussi à condition que tu fasses un effort pour comprendre.. sinon ça sert vraiment à rien franchement.
alexialj a écrit:Bonjour j’ai un devoir à rendre pour demain et je bloque sur un exercice qui est de résoudre dans R les inéquations suivantes en détaillant les calculs :
A) -6x*2 + 4x + 2 inférieur à 0
B) 3 x sur 1-x inférieur ou égal à 0
C) -4x*2 + 4x - 1 sur x-3 supérieur a 0
D) 16-x*2 sur x*2-x-6 inférieur ou égal à 0
Pourriez vous m’aider ?
A toi de rédiger proprement...
A) On factorise
Donc le trinome de degré 2,
En conclusion, l'ensemble des solutions est :
B) 3x/(1 - x) < 0
Cette inéquation est définie pour tout x différent de 1.
On a 3x < 0 pour x < 0
et (1 - x)< 0 pour x > 1
Donc (tableau de signes) l'ensemble des solutions est:
C) Factorisons: -4x*2 + 4x - 1 . On constate une identité remarquable:
L
On étudie le signe du dénominateur, (x - 3) > 0 lorsque x>3. et (x - 3) < 0 lorsque x < 3
donc l'ensemble des solutions est
D) Factorisons le numérateur, on a une identité remarquable (16 - x^2) = (4 - x)(4 + x)
Par ailleurs, factorisons x^2-x-6 a pour discriminant delta = 25, donc deux solutions etc... donc la factorisation est
L'inéquation n'est donc pas définie en x = -2 et x = 3
On a donc le tableau de signes suivant (tu traces le tableau avec les nombres 4, -4, -2 et 3 rangés par ordre et tu marques les signes de chaque terme. Regarde sur le net comment on présente le tableau.
On conclut que l'ensemble des solutions est
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Résoudre dans R inéquations
alexialj a écrit:Si j’ai 14 je remonterais à 6,5-7
Voilà.. tu as de quoi te remonter jusqu'à 8 .. je tai mis toutes les réponses.. mais c'est une exception.. et c'est juste pour te dépanner.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
33 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
