Relations d'Al-Kashi & formule des sinus
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Emel-ii-nee
- Membre Naturel
- Messages: 52
- Enregistré le: 15 Fév 2010, 19:25
-
 par Emel-ii-nee » 02 Avr 2010, 18:06
par Emel-ii-nee » 02 Avr 2010, 18:06
J'ai un petit soucis avec un exercice, et j'aurais besoin de votre aide..
Voici l'énoncé :
Soit ABC un triangle. On utilise les notations du théorème d'Al-Kashi.
1°) Démontrer que l'aire S de ABC peut s'écrire : S = 1/2bc sinA
2°) Déterminer deux autres ralations analogiques à celle du 1°, et établir la "formule de sinus" : a/sinA = b/sinB = c/sinC = abc/2S.
3°) a) On donne BC = 1 = 6, B = 45° et C = 75°
Déterminer la valeur exacte de b, puis celle de c, en utilisant a² = b² + c² - 2bc cosA.
b) On donne c = 10,5, b = 12 et C = 60°
Résoudre dans R l'équation d'inconnue a.
c² = a² + b² - 2ab cosC
Combien de triangles obtient-on ?
Les triangles obtenus sont-ils isométriques ?Merci d'avance..


-
Hiphigenie
- Membre Relatif
- Messages: 354
- Enregistré le: 20 Déc 2009, 09:14
-
 par Hiphigenie » 02 Avr 2010, 18:30
par Hiphigenie » 02 Avr 2010, 18:30
Bonjour,
a) On va d'abord étudier le cas où les 3 angles sont aigus.
Tu traces la hauteur [CH] perpendiculaire à [AB].
Alors l'aire S = 1/2 AB.CH.
Tu calcules la valeur de sinA dans le triangle rectangle AHC et tu auras presque terminé.

-
Emel-ii-nee
- Membre Naturel
- Messages: 52
- Enregistré le: 15 Fév 2010, 19:25
-
 par Emel-ii-nee » 03 Avr 2010, 16:07
par Emel-ii-nee » 03 Avr 2010, 16:07
Voici la réponse que je propose :
1°) On sait que S = (base*hauteur)/2.
On trace la hauteur H issue de C. L'air du triangle est donc égale à S = (AB*CH)/2
Or CH = AC sin  = b sin  et AB = c
d'où S = (1/2)bc*sinÂAinsi, pour la
2°), je reprend la même démarche :
On trace la hauteur G issue de A. L'air du triangle est donc égale à S = (BC*AG)/2
Or AG = BA sin B = c sin B et BC = a
d'où S = (1/2)ca*sinB.
De même, on trace la hauteur J issue de B. L'air du triangle est donc égale à S = (AC*BJ)/2
Or BJ = CB sin C = a sin C et CA = b
d'où S = (1/2)ab*sinC
Ainsi, on peut écrire que a/sinA = b/sinB = c/sinC = abc/2S. Qu'en pensez vous ?


-
Hiphigenie
- Membre Relatif
- Messages: 354
- Enregistré le: 20 Déc 2009, 09:14
-
 par Hiphigenie » 03 Avr 2010, 17:33
par Hiphigenie » 03 Avr 2010, 17:33
Au lieu de ceci :
On trace la hauteur H issue de C.
On trace la hauteur G issue de A
De même, on trace la hauteur J issue de B
je dirais :
On trace la hauteur issue de C perpendiculaire à [AB] au point H. On trace la hauteur issue de A perpendiculaire à [BC] au point G. De même, on trace la hauteur issue de B perpendiculaire à [AC] au point J. La raison est que la hauteur ne peut pas être définie par un point comme tu le présentais.
L'air du triangle
Un triangle ne respire pas d'air mais il a une
aire .... :doh:
Ainsi, on peut écrire que a/sinA = b/sinB = c/sinC = abc/2S.
C'est une conclusion un peu hâtive puisque tu ne l'as pas démontrée comme il était demandé dans l'énoncé.
-
Emel-ii-nee
- Membre Naturel
- Messages: 52
- Enregistré le: 15 Fév 2010, 19:25
-
 par Emel-ii-nee » 04 Avr 2010, 22:07
par Emel-ii-nee » 04 Avr 2010, 22:07
Ainsi, on peut écrire que S = 1/2 bc sin donc sin = 2S/bc d'où
a/sin = a / [2S/bc] = a * (bc/2S) = abc/2S
Donc a/sinA = b/sinB = c/sinC = abc/2S.
:)

-
Hiphigenie
- Membre Relatif
- Messages: 354
- Enregistré le: 20 Déc 2009, 09:14
-
 par Hiphigenie » 04 Avr 2010, 22:16
par Hiphigenie » 04 Avr 2010, 22:16
Oui, ainsi c'est moins hâtif comme conclusion...
Si on veut être complet dans la résolution, il faudrait l'adapter également aux deux autres égalités de S.
(S = 1/2 ac sinB et S = 1/2ab sinC)

-
Hiphigenie
- Membre Relatif
- Messages: 354
- Enregistré le: 20 Déc 2009, 09:14
-
 par Hiphigenie » 04 Avr 2010, 22:27
par Hiphigenie » 04 Avr 2010, 22:27
Cela me fait penser que tu nas traité que le 1er cas du post du 02/04 à 19h30. Il faut également envisager le 2ème cas où un des angles est obtus. Il ny a pas grand-chose à changer dans la démonstration. Or CH = AC sin  = b sin Â
[font=Calibri]
Il faudra écrire : [/font]
Or CH = AC sin (CÂB) = b sin (CÂB) = b sin([font=Calibri][font=Calibri];)[/font][/font] - Â) = b sin Â
-
Emel-ii-nee
- Membre Naturel
- Messages: 52
- Enregistré le: 15 Fév 2010, 19:25
-
 par Emel-ii-nee » 05 Avr 2010, 17:55
par Emel-ii-nee » 05 Avr 2010, 17:55
Très bien, merci.
Ensuite, pour la question 3°), c'est une application. Mais j'aurais besoin de votre aide pour me guidé...
De plus, qu'est-ce q'un triangle isométriques ?
Merci d'avance.

-
Hiphigenie
- Membre Relatif
- Messages: 354
- Enregistré le: 20 Déc 2009, 09:14
-
 par Hiphigenie » 05 Avr 2010, 19:15
par Hiphigenie » 05 Avr 2010, 19:15
Je voudrais bien te répondre mais il y a un problème dans l'énoncé.
3°) a) On donne BC = 1 = 6, B = 45° et C = 75°
Pour ta deuxième questions,
deux triangles sont isométriques si leurs 3 côtés sont respectivement égaux.
-
Emel-ii-nee
- Membre Naturel
- Messages: 52
- Enregistré le: 15 Fév 2010, 19:25
-
 par Emel-ii-nee » 05 Avr 2010, 23:31
par Emel-ii-nee » 05 Avr 2010, 23:31
Désolée, j'ai fais une erreur dans l'énoncé.
Ce n'est pas [strike]BC = 1 = 6[/strike]
mais : BC = a = 6
Mais en faite, comment déterminer les valeurs de b et c, avec la formule qu'ils donnent ?
Je vais essayé quelque chose, mais je ne suis pas sûr du tout..
a) a² = b² + c² - 2bc cosÂ
d'où 6² = b² + c² - 2bc cosÂ
Mais je reste bloquée là.
A quoi pourrait servir les angles B et C dans notre calcul ?

-
Hiphigenie
- Membre Relatif
- Messages: 354
- Enregistré le: 20 Déc 2009, 09:14
-
 par Hiphigenie » 05 Avr 2010, 23:47
par Hiphigenie » 05 Avr 2010, 23:47
[font=Calibri]Non, tu as raison cest impossible par cette relation même si tu sais que  = 60° (la somme des 3 angles = 180° et que la somme des deux autres = 45° + 75° = 120°)[/font]
[font=Calibri]Il faut plutôt utiliser la relation aux sinus que tu as démontrée au 2°) grâce au théorème dAl-Kashi.[/font]
[font=Calibri]Cela fonctionne assez facilement.[/font]
-
Emel-ii-nee
- Membre Naturel
- Messages: 52
- Enregistré le: 15 Fév 2010, 19:25
-
 par Emel-ii-nee » 06 Avr 2010, 15:59
par Emel-ii-nee » 06 Avr 2010, 15:59
Donc..
A = 180 - (75+45) = 60°
De plus, a/sinA = b/sinB d'où b = (a * sinB)/sinA = (6 * sin45)/sin60
Je trouve b à peu près = à 5.
Ensuite, on remplace dans a² = b² + c² - 2bc cosÂ
soit c² = a² + b² - 2ab cos C.
On a c² = 6² + 5² - 2*6*5 * cos75
Je trouve = à peu près = à 0,07. Il y a une erreur quelque part, mais je ne l'a trouve pas.. :S
Merci d'avance.

-
Hiphigenie
- Membre Relatif
- Messages: 354
- Enregistré le: 20 Déc 2009, 09:14
-
 par Hiphigenie » 06 Avr 2010, 20:20
par Hiphigenie » 06 Avr 2010, 20:20
b = (a * sinB)/sinA = (6 * sin45)/sin60
Je trouve b à peu près = à 5.
[font=Calibri]Il faut travailler avec les valeurs exactes. Elles seront encore utilisées par la suite
[/font] [font=Calibri] [/font]
[/font] Donc :
 [font=Calibri]Pour le 3°, tu nas pas respecté la consigne : [/font]
[font=Calibri]Pour le 3°, tu nas pas respecté la consigne : [/font] [font=Calibri]
[/font]3°) a) On donne BC = a = 6, B = 45° et C = 75°
Déterminer la valeur exacte de b, puis celle de c en utilisant a² = b² + c² - 2bc cosA.
a² = b² + c² - 2bc cosA 
 [color=black]
[color=black]
[/color]
[font=Calibri]

[/font]
[font=Calibri]Cest une équation du 2nd degré. Calcul de [/font];)[font=Calibri]
. etc
[/font] [font=Calibri]

[/font]
-
Emel-ii-nee
- Membre Naturel
- Messages: 52
- Enregistré le: 15 Fév 2010, 19:25
-
 par Emel-ii-nee » 07 Avr 2010, 21:07
par Emel-ii-nee » 07 Avr 2010, 21:07
D'accord, voici le travail que j'ai fais :
3°)a) Suite..
Ainsi, Delta = b² - 4ac = 72
et  Delta = 3;)8.
Delta = 3;)8.
c1 = (-b +  Delta)/2a = - (-2;)6 + 3;)8) / 2*1
Delta)/2a = - (-2;)6 + 3;)8) / 2*1
c2 = (-b -  Delta)/2a = - (-2;)6 - 3;)8) / 2*1
Delta)/2a = - (-2;)6 - 3;)8) / 2*1Mais avec toutes ces racines carrées, je ne m'en sors pas et je n'arrive pas à poursuivre mon calcul..
Merci d'avance.

-
Hiphigenie
- Membre Relatif
- Messages: 354
- Enregistré le: 20 Déc 2009, 09:14
-
 par Hiphigenie » 07 Avr 2010, 21:22
par Hiphigenie » 07 Avr 2010, 21:22
-
Emel-ii-nee
- Membre Naturel
- Messages: 52
- Enregistré le: 15 Fév 2010, 19:25
-
 par Emel-ii-nee » 08 Avr 2010, 00:19
par Emel-ii-nee » 08 Avr 2010, 00:19
On peut en conclure que :
6² = (2;)6)² + (;)6 + 3;)2)² - 2 * (2;)6) * (;)6 + 3;)2) * cos60. ??
Ensuite, pour la b) ...
"Emel-ii-nee" a écrit:b) On donne c = 10,5, b = 12 et C = 60°
Résoudre dans R l'équation d'inconnue a.
c² = a² + b² - 2ab cosC
Combien de triangles obtient-on ?
Les triangles obtenus sont-ils isométriques ?
c² = a² + b² - 2ab cosC
(10,5)² = a² + 12² - 2*a*12 * cos60
110,25 = a² + 144 - 24a * 1/2
110,25 = a² + 144 - 12a
a² - 12a - 33,75 = 0
Ainsi Delta = (-12)² - 4*1*(-33,75) = 144 - (-135) = 279
 Delta = 3;)31 (Dites moi si on peut simplifier..)
Delta = 3;)31 (Dites moi si on peut simplifier..)
a1 = (12 + 3;)31)/2*1
a2 = (12 - 3;)31)/2*1[...]
J'attend de voir si c'est bon pour poursuivre..
Merci d'avance.

-
Hiphigenie
- Membre Relatif
- Messages: 354
- Enregistré le: 20 Déc 2009, 09:14
-
 par Hiphigenie » 08 Avr 2010, 07:59
par Hiphigenie » 08 Avr 2010, 07:59
Pourquoi ce « ?? » ?
en effet : a = 6 ;
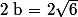
;
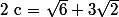
, Â = 60°
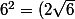^2 + (\sqrt{6} + 3\sqrt{2})^2 - 2.(2\sqrt{6})(\sqrt{6} + 3\sqrt{2}).cos60^{o})
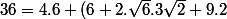 - 4\sqrt{6}(\sqrt{6} + 3\sqrt{2}).\frac{1}{2})
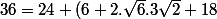 - 2\sqrt{6}(\sqrt{6} + 3\sqrt{2}))
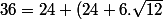 - (2.6 + 6\sqrt{12}))
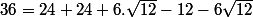
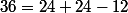
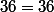
Pour le b) :
a² - 12a - 33,75 = 0
Attention : a² - 12a
+ 33,75 = 0
a = 7,5 ou a = 4,5.
-
Emel-ii-nee
- Membre Naturel
- Messages: 52
- Enregistré le: 15 Fév 2010, 19:25
-
 par Emel-ii-nee » 08 Avr 2010, 16:41
par Emel-ii-nee » 08 Avr 2010, 16:41
Conclusion : il y a 2 triangles non isométriques qui répondent à la question.

-
Hiphigenie
- Membre Relatif
- Messages: 354
- Enregistré le: 20 Déc 2009, 09:14
-
 par Hiphigenie » 08 Avr 2010, 19:07
par Hiphigenie » 08 Avr 2010, 19:07
Eh bien, es-tu heureux(se) ? :happy2:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités


 [/font]
[/font]








 .
. est à exclure car
est à exclure car  et c représente une longueur positive.
et c représente une longueur positive.