Récurrence
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
knizarim
- Messages: 4
- Enregistré le: 06 Oct 2014, 13:29
-
 par knizarim » 06 Oct 2014, 16:52
par knizarim » 06 Oct 2014, 16:52
Bonjour j'ai besoin d'aide Svp
Prouve que ;)k(4/5);)k=(4×5;);)¹;)(5+n)4;);)¹)/5
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 06 Oct 2014, 17:24
par paquito » 06 Oct 2014, 17:24
Pas de bonjour, l'impératif, tu t'es trompé de site; programme "esclave" sur ton moteur de recherche!!!
-
knizarim
- Messages: 4
- Enregistré le: 06 Oct 2014, 13:29
-
 par knizarim » 06 Oct 2014, 17:41
par knizarim » 06 Oct 2014, 17:41
paquito a écrit:Pas de bonjour, l'impératif, tu t'es trompé de site; programme "esclave" sur ton moteur de recherche!!!
Je M'excuse Mais comme je l'ai deja sité Je suis vraiment chamboulé ces derniers temps Je dois rendre plusisuers devoirs demain et je n'ai pas dormi de toutes la nuit je suis sincèrement désolé

-
mathelot
 par mathelot » 06 Oct 2014, 17:51
par mathelot » 06 Oct 2014, 17:51
pour la démonstration par récurrence, il suffit d'ajouter
(4/5)^{n+1})
des deux côtés de l'égalité de récurrence
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 06 Oct 2014, 18:01
par paquito » 06 Oct 2014, 18:01
knizarim a écrit:Bonjour j'ai besoin d'aide Svp
Prouve que

k(4/5);)k=(4×5;);)¹;)(5+n)4;);)¹)/5
Pas envie!!
-
knizarim
- Messages: 4
- Enregistré le: 06 Oct 2014, 13:29
-
 par knizarim » 07 Oct 2014, 09:46
par knizarim » 07 Oct 2014, 09:46
mathelot a écrit:pour la démonstration par récurrence, il suffit d'ajouter
(4/5)^{n+1})
des deux côtés de l'égalité de récurrence
Merci infiniment Je Dois rendre ce devoir cette aprem est son votre aide à tous je serais viré merci beaucouupp :*
-
mathelot
 par mathelot » 07 Oct 2014, 10:14
par mathelot » 07 Oct 2014, 10:14
as tu terminé finalement ?
-
mathelot
 par mathelot » 07 Oct 2014, 10:32
par mathelot » 07 Oct 2014, 10:32
non mais, allo quoi ? :mur:
-
knizarim
- Messages: 4
- Enregistré le: 06 Oct 2014, 13:29
-
 par knizarim » 07 Oct 2014, 10:49
par knizarim » 07 Oct 2014, 10:49
mathelot a écrit:non mais, allo quoi ? :mur:
Bonjour,
voilà ce que j'ai fait finalement

k(4/5);)k=(4×5;);)¹;)(5+n)4;);)¹)/5
INITIALISATION:
n=1
......
HEREDITE:
Fixons n;)1
on suppose que P(n) Est vrai
et On trouve P(n+1) Avec cette fois k allant de 1 jusqu'à n+1
ca donne
(n+1)*(4/5););)¹+(4×5;);)¹;)(5+n)4;);)¹)/5
et on termine le calcul
-
mathelot
 par mathelot » 07 Oct 2014, 11:21
par mathelot » 07 Oct 2014, 11:21
-
mathelot
 par mathelot » 07 Oct 2014, 11:37
par mathelot » 07 Oct 2014, 11:37
dans ta formule du début , le dénominateur est
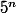
et après effectivement, ça peut se démontrer par récurrence.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
