Récurrence généralisée
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 23 Oct 2013, 18:29
par t.itou29 » 23 Oct 2013, 18:29
Bonsoir,
Je bloque complétement sur cette exo:
https://docs.google.com/file/d/0B2uj8lrnLJwSemdadFlCZTZZQzg/edit?usp=sharingA la 3a j'ai trouvé
b_{n}=\sum\limits_{i=0}^{n-1} C_{n+1}^{i} b_{i})
mais je suis pas sûr.
Pour la b je ne sais pas quoi faire, faut-il que je remplace bn par l'expression trouvée ? Ca me permettrait d'utiliser l'hypothèse de récurrence comme elle est valable juqu'à n-1, mais comment ?
Pour le lemme 4.115 il s'agit de cette inégalité (c'était la question 1 une des seules que j'ai réussies!)
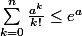
Merci de m'aider
-
keofran
- Membre Relatif
- Messages: 125
- Enregistré le: 12 Oct 2013, 00:39
- Localisation: Lyon
-
 par keofran » 23 Oct 2013, 19:40
par keofran » 23 Oct 2013, 19:40
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 23 Oct 2013, 19:47
par t.itou29 » 23 Oct 2013, 19:47
Je les connais mais je ne vois pas comment les utiliser. Dans la question 2b faut bien que je remplace bn par la somme et c'est cette somme que je dois majorer mais comment ? Si je l'écris de cette manière je peux appliquer l'hypothèse de récurrence sur les bi mais il me reste les coefficients binomiaux
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 23 Oct 2013, 20:24
par t.itou29 » 23 Oct 2013, 20:24
Je crois que je vais abandonner, je comprends vraiment mais vraiment pas !
Personne pour me donner une piste ?
-
keofran
- Membre Relatif
- Messages: 125
- Enregistré le: 12 Oct 2013, 00:39
- Localisation: Lyon
-
 par keofran » 23 Oct 2013, 21:11
par keofran » 23 Oct 2013, 21:11
Désolé je ne vois pas. Ce qui m'interpelle c'est pourquoi 4/5 et pas 3/4 ou 2/3. Il doit y avoir une raison et c'est peut-être la clé.
Je n'ai pas calculé les premiers termes mais c'est parfois en les calculant qu'on trouve une certaine "logique" qui aide pour la suite.
-
keofran
- Membre Relatif
- Messages: 125
- Enregistré le: 12 Oct 2013, 00:39
- Localisation: Lyon
-
 par keofran » 23 Oct 2013, 21:52
par keofran » 23 Oct 2013, 21:52
Je trouve :
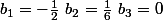
Ta formule de 3a me semble juste.
Pour la suite j'ai :
!}{(n+1-i)!} \times \left (\frac{4}{5} \right)^i)
donc :
!} \times \left (\frac{4}{5} \right)^i)
Donc :
^n))
A vérifier tout ça, en espérant faire avancer le schmilblick. Mais je ne vois pas la suite.
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 24 Oct 2013, 08:55
par t.itou29 » 24 Oct 2013, 08:55
keofran a écrit:Je trouve :
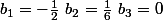
Ta formule de 3a me semble juste.
Pour la suite j'ai :
!}{(n+1-i)!} \times \left (\frac{4}{5} \right)^i)
donc :
!} \times \left (\frac{4}{5} \right)^i)
Donc :
^n))
A vérifier tout ça, en espérant faire avancer le schmilblick. Mais je ne vois pas la suite.
J'avais trouvé quelque chose de similaire à ta première inégalité mais avec i! au dénominateur.
Comme pour la 3c il demande d'utiliser

, il faut donc trouver une expression avec une somme de la forme
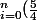^k \frac{1}{k!})
mais pour obtenir 5/4 au lieu de 4/5 je sais pas comment faire
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
