Rectangle dans un demi-cercle
15 messages
- Page 1 sur 1
Rectangle dans un demi-cercle
Bonjour à tous, je n'arrive pas à faire cet exercice:
On considère un segment [AB] de longueur 6, de milieu O. On trace un demi-cercle de diamètre [AB]. M est un point variable sur [OA] et on appelle x la distance OM. On trace le rectangle MNPQ avec N et P sur le demi-cercle et Q le symétrique de M par rapport à O.
1. Faire une figure en utilisant un logiciel de géométrie dynamique.
2. Représenter la fonction donnant l'aire du rectancle en fonction de x.
3. Conjectuer l'aire maximale du rectangle et la valeur de x correspondant.
4. Quel est l'intervalle de variation de x ?
5. Exprimer le côté MN puis l'aire du rectangle en fonction de x.
6. Démontrer votre conjecture, en montrant que le problème revient à résoudre l'inéquation: 4x²-36x²+81;) 0
7. On veut que l'aire du rectangle soit égale à la moitié de celle du demi-cercle. Conjecturer la ou les valeurs répondant au problème.
8.Montrer que ce dernier problème revient à résoudre 4x4-36x²+81/16;)²=0
Démonter votre conjecture.
J'ai juste reussi à faire la figure sur le logiciel mais après je ne comprend rien, je pense que c'est aussi un problème de français... Pouvez-vous m'aider?
On considère un segment [AB] de longueur 6, de milieu O. On trace un demi-cercle de diamètre [AB]. M est un point variable sur [OA] et on appelle x la distance OM. On trace le rectangle MNPQ avec N et P sur le demi-cercle et Q le symétrique de M par rapport à O.
1. Faire une figure en utilisant un logiciel de géométrie dynamique.
2. Représenter la fonction donnant l'aire du rectancle en fonction de x.
3. Conjectuer l'aire maximale du rectangle et la valeur de x correspondant.
4. Quel est l'intervalle de variation de x ?
5. Exprimer le côté MN puis l'aire du rectangle en fonction de x.
6. Démontrer votre conjecture, en montrant que le problème revient à résoudre l'inéquation: 4x²-36x²+81;) 0
7. On veut que l'aire du rectangle soit égale à la moitié de celle du demi-cercle. Conjecturer la ou les valeurs répondant au problème.
8.Montrer que ce dernier problème revient à résoudre 4x4-36x²+81/16;)²=0
Démonter votre conjecture.
J'ai juste reussi à faire la figure sur le logiciel mais après je ne comprend rien, je pense que c'est aussi un problème de français... Pouvez-vous m'aider?
bonjour,
indications
si désigne la hauteur du rectangle, une relation de Pythagore lie
désigne la hauteur du rectangle, une relation de Pythagore lie  et
et 
on risque d'avoir à maximiser une fonction du style
= ax \sqrt{b^2-x^2})
de deux choses , l'une
- ou, tu connais les dérivées
- ou, tu maximises le carré de)
(vû que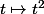 est croissante strictement et continue sur R+
est croissante strictement et continue sur R+
^2 \} = \left(\sup_{x \in [0;3]} |f(x)| \right)^2) )
)
le carré de S(x),^2) , étant un trinome de la variable
, étant un trinome de la variable 
indications
si
on risque d'avoir à maximiser une fonction du style
de deux choses , l'une
- ou, tu connais les dérivées
- ou, tu maximises le carré de
(vû que
le carré de S(x),
-----début de l'exemple --------------------------
imagine qu'une quantité U prenne les valeurs positives
3 5 2 7 4
son carré va prendre les valeurs
9 25 4 49 16
Le maximum de U est 7 et le maximum de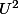 est 49
est 49
--------fin de l'exemple-------------------------------
Comme=2x \sqrt{9-x^2})
cherche le maximum de) , c'est plus facile car c'est un trinome de la variable
, c'est plus facile car c'est un trinome de la variable 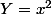
^2=4x^2(9-x^2)=4Y(9-Y)=36Y-4Y^2)
imagine qu'une quantité U prenne les valeurs positives
3 5 2 7 4
son carré va prendre les valeurs
9 25 4 49 16
Le maximum de U est 7 et le maximum de
--------fin de l'exemple-------------------------------
Comme
cherche le maximum de
mathelot a écrit:-----début de l'exemple --------------------------
imagine qu'une quantité U prenne les valeurs positives
3 5 2 7 4
son carré va prendre les valeurs
9 25 4 49 16
Le maximum de U est 7 et le maximum deest 49
--------fin de l'exemple-------------------------------
Comme
cherche le maximum de, c'est plus facile car c'est un trinome de la variable
On écrit
Le maximum de S(x) (sans carré) vaut donc
vérification avec la fonction dérivée
s'annule pour
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

