bonjour
https://imgur.com/RVBxprL
Q2 , comment trouvé la raison? 1/2^2
merci
Raison d'une suite
5 messages
- Page 1 sur 1
Re: raison d'une suite
par Ben314 » 04 Fév 2020, 19:07
Salut.
La raison de quoi ?
Si c'est la raison de la suite donnée par l'énoncé, ben chercher la raison d'une telle suite, c'est très exactement la même chose que de chercher les dents d'une poule.
La raison de quoi ?
Si c'est la raison de la suite donnée par l'énoncé, ben chercher la raison d'une telle suite, c'est très exactement la même chose que de chercher les dents d'une poule.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: raison d'une suite
par mathelot » 04 Fév 2020, 19:14
bonsoir,
pose l'hypothèse de récurrence au rang n sous forme d'inégalité puis ajoute^2)
à chaque membre
Ps:il n'y a pas de raison. Le terme général u_n est la somme de n termes. La notation avec les petits points est conventionnelle. A chaque itération, on rajoute un terme à la somme
pose l'hypothèse de récurrence au rang n sous forme d'inégalité puis ajoute
Ps:il n'y a pas de raison. Le terme général u_n est la somme de n termes. La notation avec les petits points est conventionnelle. A chaque itération, on rajoute un terme à la somme
Re: raison d'une suite
par mathelot » 06 Fév 2020, 22:19
Question 1
La différence
vaut ^2})
La suite de terme général)
est strictement croissante
Question 2
soit l'hypothèse de récurrence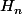
: 
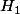se résume à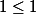 
l'hypothèse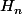 est vérifiée au rang 1.
supposons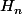
on ajoute^2})
aux deux membres de l'inégalité:
^2} \leq 2- \frac{1}{n} +\frac{1}{(n+1)^2})
^2} \leq 2-\frac{1}{n+1})
en effet
^2} \leq - \frac{1}{n+1})
équivaut à
^2} \leq \frac{1}{n})
équivaut à
^2} \leq \frac{1}{n})
équivaut à
 \leq (n+1)^2)
qui est vraie.
l'hypothèse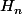 est héréditaire pour 
en conclusion du raisonnement par récurrence, on obtient
question 3
la suite (u_n) à termes réels est strictement croissante et majorée par 2.
elle converge.
On montre que sa limite est
La différence
La suite de terme général
Question 2
soit l'hypothèse de récurrence
l'hypothèse
supposons
on ajoute
en effet
l'hypothèse
en conclusion du raisonnement par récurrence, on obtient
question 3
la suite (u_n) à termes réels est strictement croissante et majorée par 2.
elle converge.
On montre que sa limite est
Re: raison d'une suite
par mathelot » 06 Fév 2020, 23:02
pour 
, on a de manière évidente
} \leq \dfrac{1}{n^2} \leq \dfrac{1}{n(n-1)})
soit
en sommant ces inégalités de n=2 à n=N, il vient:
en ajoutant 1
soit
en sommant ces inégalités de n=2 à n=N, il vient:
en ajoutant 1
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :