Racine double
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
AnA92
- Membre Naturel
- Messages: 21
- Enregistré le: 11 Jan 2009, 21:03
-
 par AnA92 » 17 Jan 2009, 04:15
par AnA92 » 17 Jan 2009, 04:15
Bonjour;
Alors voilà j'ai tombé sur un exo que je ne vois pas comment le résoudre même que j'ai plein d'idées... mais bon je veux savoir vos indications aussi:
L'exo est :
Déterminer µ tel que
=x^3-3x)
+µ ait une racine double.
Des idées SVP??
-
Florélianne
- Membre Rationnel
- Messages: 641
- Enregistré le: 06 Sep 2008, 20:23
-
 par Florélianne » 17 Jan 2009, 08:05
par Florélianne » 17 Jan 2009, 08:05
Bonjour,
Déterminer µ tel que  +µ ait une racine double.
+µ ait une racine double.
tu peux dire que si P(x) a une racine double alors
P(x) = (x-a)²(x-b)
du développes et tu identifies... (j'ai déjà mis le coefficient des "x" à 1 pour obtenir x^3)
ensuite ça va tout seul !
Très cordialement

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 17 Jan 2009, 13:16
par leon1789 » 17 Jan 2009, 13:16
On peut aussi utiliser le pgcd de P et P' (mais est-ce au programme du lycée ? je doute)
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 17 Jan 2009, 14:05
par XENSECP » 17 Jan 2009, 14:05
leon1789 a écrit:On peut aussi utiliser le pgcd de P et P' (mais est-ce au programme du lycée ? je doute)
Lol inutile de se compliquer la vie ^^

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 17 Jan 2009, 15:21
par leon1789 » 17 Jan 2009, 15:21
XENSECP a écrit:Lol inutile de se compliquer la vie ^^
Justement, très souvent, le pgcd de P,P' fonctionne nettement mieux qu'une identification avec de multiples inconnues provenant d'une factorisation formelle ! Tu es d'accord ??
Mais il est vrai que l'exo en cours est un contre-exemple à ce que je dis : normal, le pgcd P, P' n'est pas au programme de Term. Donc une autre solution (en l'occurrence celle de Florélianne) est la bonne à suivre.
-
AnA92
- Membre Naturel
- Messages: 21
- Enregistré le: 11 Jan 2009, 21:03
-
 par AnA92 » 17 Jan 2009, 16:51
par AnA92 » 17 Jan 2009, 16:51
Bein je suis en terminal mais même celà je sais bien c'est quoi le PGCD de deux Polynomes :++: d'autre part c'est quoi P' ??
Pour la méthode que Florélianne m'a indiqué je trouve a= i et b=-2i d'où µ=2i c'est bien ça??

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 17 Jan 2009, 16:57
par leon1789 » 17 Jan 2009, 16:57
AnA92 a écrit:Bein je suis en terminal mais même celà je sais bien c'est quoi le PGCD de deux Polynomes :++:
ah bon, tu sais ce que c'est ?! tu es en terminale en france ?
AnA92 a écrit:d'autre part c'est quoi P' ??
ben c'est la dérivée de P !!
AnA92 a écrit:Pour la méthode que Florélianne m'a indiqué je trouve a= i et b=-2i d'où µ=2i c'est bien ça??
le i de i²=-1 ? non pas du tout. Tu as fait une petite erreur de signe
-
AnA92
- Membre Naturel
- Messages: 21
- Enregistré le: 11 Jan 2009, 21:03
-
 par AnA92 » 17 Jan 2009, 17:10
par AnA92 » 17 Jan 2009, 17:10
Je vous détaille mon calcul:
P(x)=(x²-2ax+a²)(x-b)
=

-bx²-2ax²+2abx+a²x-ba²
=

+x²(-b-2a)+x(2ab+a²)-ba²
=>b+2a=0 cela donne b=-2a
et 2ab+a²=3 => a²-4a²=3 => -3a²=3 d'où a²=-1 donc
a=i aussi b=-2i =>
µ=-2i mnt c'est bien (j'ai pas fait attention que µ=
-ba².
Pour le PGCD qu'elle est la relation entre PGCD et P' car à la fin ce que je connais de pgcd de deux polynome c'est les division successsif de quotient sur le reste ???!!!

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 17 Jan 2009, 17:28
par leon1789 » 17 Jan 2009, 17:28
AnA92 a écrit:Je vous détaille mon calcul:
P(x)=(x²-2ax+a²)(x-b)
=

-bx²-2ax²+2abx+a²x-ba²
=

+x²(-b-2a)+x(2ab+a²)-ba²
=>b+2a=0 cela donne b=-2a
et 2ab+a²=3
non 2ab+a²=
-3 :zen:
AnA92 a écrit:Pour le PGCD qu'elle est la relation entre PGCD et P' car à la fin ce que je connais de pgcd de deux polynome c'est les division successsif de quotient sur le reste ???!!!
Sais-tu que
>
?
-
Florélianne
- Membre Rationnel
- Messages: 641
- Enregistré le: 06 Sep 2008, 20:23
-
 par Florélianne » 17 Jan 2009, 18:56
par Florélianne » 17 Jan 2009, 18:56
Bonsoir,
Je n'ai trouvé (ce matin) qu'une seule valeur de mu possible : mu = 0 dans IR! la racine double étant V3 et 0 la simple !
dans les autres cas le discriminant était négatif...
mais devait-on résoudre dans C ?
Et laisse les experts discuter ensemble... chaque chose en son temps ^_*
Très cordialement...

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 17 Jan 2009, 19:05
par leon1789 » 17 Jan 2009, 19:05
Florélianne a écrit:Bonsoir,
Je n'ai trouvé (ce matin) qu'une seule valeur de mu possible : mu = 0 dans IR! la racine double étant V3 et 0 la simple !
dans les autres cas le discriminant était négatif...
mais devait-on résoudre dans C ?
Et laisse les experts discuter ensemble... chaque chose en son temps ^_*
Très cordialement...
ben les experts diront que tu as fait une faute de calcul ! c'est évidemment pas µ=0 ...
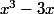
a 3 racines simples !
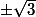
et 0
Très cordialement...
--> il y a deux valeurs (entières) de µ qui donnent une racine double au polynôme.
-
Florélianne
- Membre Rationnel
- Messages: 641
- Enregistré le: 06 Sep 2008, 20:23
-
 par Florélianne » 17 Jan 2009, 22:26
par Florélianne » 17 Jan 2009, 22:26
Bonsoir,
Tout à fait exact, j'ai fait de tête et trop vite !
De toute façon, je ne tenterai pas de recommencer ce soir, je suis dans le brouillard! alors si l'erreur est humaine, inutile d'en rajouter dans l'humanité... quand au souvenir de mes calculs, il y avait une équation de degré 2 au discriminant négatif... mais rien ne dit que c'était juste... aucune trace ! L'ennui de faire de tête...
Encore toutes mes excuses !
Je n'ai plus l'âge de faire de tête !
Bonne chance pour la résolution, de toute façon, aujourd'hui je suis nettement au dessous de tout !
Bonne nuit

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 18 Jan 2009, 13:41
par leon1789 » 18 Jan 2009, 13:41
Les calculs de AnA92 étaient justes, sauf qu'il y avait une erreur de signe "de recopiage" de l'énoncé. Du coup, on tombe sur a²=1 (et non a²=-1...)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
-bx²-2ax²+2abx+a²x-ba²
+x²(-b-2a)+x(2ab+a²)-ba²