Bonjour,
J'aurais deux questions concernant la formulation en mathématiques.
1. Lorsqu'on écrit (par exemple dans le deuxième critère d'une caractérisation de base topologique, notée

:

(ceci pour
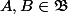
) à quel moment précise-t-on que le

dépend de

?
On aurait tout bien pu interpréter cette expression (telle qu'elle est écrite) en voyant

comme un ensemble ne dépendant pas de

. Ça peut paraitre bête mais j'ai fait la faute tout à l'heure en concluant que
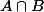
était inclus dans

. Comment différencier en terme de notation le cas où

dépend de

et le cas où il ne dépend pas de

? Faut-il partir du principe qu'il dépend toujours de

et que, seulement sur indication expressément faite, il ne dépendra pas de

?
2. Autre "imprécision" (à mon sens) dans la formulation mathématique : lorsque l'on écrit la négation de
)
(qui n'est autre que la négation de
)
), on devrait avoir quelque-chose de l'ordre de "il existe (au moins) un contre-exemple" (c'est à dire (au moins) un

tel que
)
ne soit pas vérifiée). Or la négation d'une telle implication s'écrit ainsi :
)
. Or je ne sais pas vraiment comment interpréter ce qui est à gauche du ET logique : je lis

appartient à

mais en quoi cela garantit-il qu'il en existe (au moins) un ? Peut-être que l'existence même d'un représentant de

(existence sous-entendue par
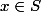
) garantit-elle qu'il y a au moins un représentant ?
Pourriez-vous m'indiquer si mes suppositions sont vraies ?
Merci beaucoup
Très bonne journée.
