Quelle règle pour une équation ?

[Octarine]

Bonjour !

D'après la règle : a - b = - ( b - a )
et celle : ( a + b ) ( a + b ) = ( a + b )^2

Je ne sais pas comment résoudre le premier produit de l'équation : - ( - 2x + 3 ) ( 2x + 3 ) + 2 ( 2x - 3 ) ( 4x - 12 )

Je pense que concernant les règles des signes mes connaissances sont également justes
H.E.L.P

[zygomatique]

salut

avant tout il serait bien de voir un facteur commun ...

[Octarine]

Je voudrais bien le faire, mais dans la mesure où je ne vois pas comment...

[Lostounet]

Bonjour !

D'après la règle : a - b = - ( b - a )
et celle : ( a + b ) ( a + b ) = ( a + b )^2

Je ne sais pas comment résoudre le premier produit de l'équation : - ( - 2x + 3 ) ( 2x + 3 ) + 2 ( 2x - 3 ) ( 4x - 12 )

Je pense que concernant les règles des signes mes connaissances sont également justes
H.E.L.P

Salut,
D'abord il faut juste préciser que ceci n'est pas une équation (on a pas une égalité dans laquelle on cherche à trouver la valeur de x (ie la résoudre) telle que l'égalité soit vraie, du style 2x = 10) mais une expression littérale (ou une fonction de x). Si on la transforme (en factorisant ou développant), elle doit rester vraie pour toute valeur de x. Il faut donc que tu nous dises si tu veux développer l'expression, ou bien la factoriser !

Si tu as oublié ce que cela veut dire, tu peux regarder mon guide de rappel ici: college-primaire/developper-factoriser-t120839.html

Cela dit, la difficulté majeure réside dans ce "-" qui est au début, non? Ce que tu peux faire, c'est constater que prendre l'opposé d'un nombre, c'est le multiplier par (-1). Cela signifie que:


Mais il y a aussi un autre facteur caché ! Si tu observes bien, on constate que

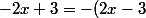Si bien que l'expression devient


Cela permet de mettre en évidence (2x - 3) qui est le facteur commun ! et de factoriser l'expression si c'est le but.

[Octarine]

Si tu as oublié ce que cela veut dire, tu peux regarder mon guide de rappel ici: college-primaire/developper-factoriser-t120839.html

prendre l'opposé d'un nombre, c'est le multiplier par (-1)

Merci pour le rappel, j'ai tout regardé et ça m'a fait du bien !

Je m'excuse pour le manque de précision, ma consigne est de "développer et réduire", grâce à vos indications j'en suis venue à :

- ( - 2x + 3 ) ( 2x + 3 ) + 2 ( 2x - 3 ) ( 4 x - 12 )
= ( - 1 ) ( - 1 ) ( 2x - 3 ) ( 2x + 3 ) + 2 ( 8x^2 - 24x - 12x + 36 )
= ( 2x - 3 ) ( 2x + 3 ) + 16x^2 - 48x - 24x + 72 )
= 2x^2 - 3^2 + 16x^2 - 72x + 72
=18x^2 - 72x + 66

Cela ne fonctionne toujours pas je commence réellement à désespérer

[Lostounet]

Salut!

Je suis à Milano mais je réponds quand même :p

(2x-3)(2x+3) est de la forme (a-b)(a+b) = a^2-b^2
avec a = 2x et b= 3
Ce qui signifie que a^2=(2x)^2=4x^2 et non pas 2x^2

Et puis 72-9=63 pas 66

[Octarine]

C'est génial j'ai enfin résolu cette expression que je me traine depuis 5 jours + appris beaucoup de choses, je vous laisse profiter de vos vacances à Milano !! Merci

[laetidom]

Bonjour,

Sauf erreur :

- ( - 2x + 3 ) ( 2x + 3 ) + 2 ( 2x - 3 ) ( 4 x - 12 ) :

- ( - 2x + 3 ) = - (-2x) - (3) = 2x - 3

(2x-3)(2x+3) = 2x.2x + 2x.3 - 3.2x - 3.3 = 4x² + 6x - 6x - 9 = 4x² - 9

2 ( 2x - 3 ) ( 4 x - 12 ) = 2 [ 2x.4x + 2x.(-12) - 3.4x + (-3)(-12)] = 2(8x² - 24x - 12x + 36) = 2(8x² - 36x + 36) = 16x² - 72x + 72

4x² - 9 + 16x² - 72x + 72 = 20x² - 72x +63

[Octarine]

= 20x² - 72x +63

J'ai trouvé la même chose, merci pour la confirmation !

[laetidom]

Génial !!

Pour la factorisation c'est ok ?


(Bon voyage à Lostounet en Italie)

[laetidom]

= 20x² - 72x +63

J'ai trouvé la même chose, merci pour la confirmation !

Petite astuce de contrôle de la justesse de ton expression trouvée :

Dans geogebra, tu saisis dans la ligne de commande en bas de l'écran : y = -(-2x+3)(2x+3)+2(2x-3)(4x-12), tu valides et le logiciel réduis l'expression à y = 20x² - 72x + 63 ====> ça confirme !!