Bonjour je n'arrive pas du tout a faire cette exercice. Le professeur nous l'a donné comme cela. Je n'ai rien commencé car je ne comprends rien. Pouvez-vous m'aider s'il vous plait ? Merci d'avance.
Démontrer que , pour tout réel x, on a :
e-x - e-2x = ex - 1/e2x
Propriétés algébriques
10 messages
- Page 1 sur 1
Re: Propriétés algébriques
Tu voulais écrire
 , c'est bien ça ??
, c'est bien ça ??
Il y a des propriétés de l'exponentielle que tu connais sûrement :
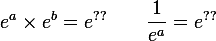 .
.
Il y a des propriétés de l'exponentielle que tu connais sûrement :
Re: Propriétés algébriques
ah bon ? il faut que j'utilse c'est deux formules pour ça e-x - e-2x = ex - 1/e2x ?
Re: Propriétés algébriques
Oui bien sûr. Ce sont les propriétés fondamentales de l'exponentielle.
Alors, qu'attends-tu pour traiter cet exercice ?
Alors, qu'attends-tu pour traiter cet exercice ?
Re: Propriétés algébriques
Bonjour,
moi, je serai toi, je commencerai par mettre e^(-x) et e^(-2x) sous forme de fractions, puis mise au même dénominateur, puis mise en facteurs, puis simplification.
moi, je serai toi, je commencerai par mettre e^(-x) et e^(-2x) sous forme de fractions, puis mise au même dénominateur, puis mise en facteurs, puis simplification.
Re: Propriétés algébriques
Mouais... je ne vois pas beaucoup d'effort de ta part, olivu. À se demander si tu n'attends pas tout simplement qu'on fasse l'exercice pour toi, ici ou sur ilemaths.
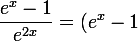 \times \dfrac1{e^{2x}} = \ldots)
Mmm... quelque chose en rapport avec les propriétés de l'exponentielle que je t'ai fait écrire ?
Mmm... quelque chose en rapport avec les propriétés de l'exponentielle que je t'ai fait écrire ?
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
