Problème trè urgent a résoudre de seconde !!!

[Anonyme]

voila je voudrai savoir comment fait on pour mettre 0.457457457... sous la forme d'une fraction de 2 entiers ??? c trè urgent pouvez vous m'expliquer svp ??? merci d'avance

[Anonyme]

Salut prend ta calculette tout d'abord pour trouver la réponse tape ton chiffre puis si ta un TI 82 tape sur maths pui frac il me semble voila

[Chimerade]

voila je voudrai savoir comment fait on pour mettre 0.457457457... sous la forme d'une fraction de 2 entiers ??? c trè urgent pouvez vous m'expliquer svp ??? merci d'avance

0.457457457 = 0,457 * (1+0.001+0.000001+0.000000001+...)



La parenthèse est la somme d'une série géométrique du type :



Le cours sur les suites dit que si |q|<1 alors cette somme tend vers :



Ici, l'expression
doit précisément être considérée comme la limite de cette somme lorsque le nombre de termes tend vers l'infini. Donc


Finalement, le nombre de départ est donc égal à :

[Nightmare]

Bonjour chimerade

Tu te compliques la vie avec les suites :

en notant a=0,457457... :
1000a=457,457457...=457+a
donc
999a=457
d'ou finalement :
a=457/999

:happy3:
Jord

[Anonyme]

Il se complique la tache mais certains prof ne veulent que ce gener de solution et non la tienne ...

[Alpha]

Bonjour à tous,

La méthode de Chimerade est plus rigoureuse. Je me souviens qu'un jour, en Terminale S, on avait eu ce genre d'exo à faire. Un élève avait proposé la solution proposée par Nightmare (que j'ai aussi proposée dans un autre post où la même question a été posée), mais notre prof n'a pas trop aimé, elle a préféré écrire une suite géométrique.

Pour être vraiment rigoureux, il faudrait calculer ce que cela donne pour , puis faire tendre vers

C'est une question de goût à mon avis.

Cordialement

[Chimerade]

Bonjour chimerade

Tu te compliques la vie avec les suites :

en notant a=0,457457... :
1000a=457,457457...=457+a
donc
999a=457
d'ou finalement :
a=457/999

:happy3:
Jord

Très juste. Pourquoi faire compliqué quand on peut faire simple diras-tu ? Je trouve ta méthode très élégante, mais la série géométrique m'a sauté à la figure avec une telle violence que je n'ai même pas vu ta méthode que je considère bien plus élégante.
Merci de ma la rappeler.

[Chimerade]

La méthode de Chimerade est plus rigoureuse.

C'est gentil, mais inexact ! Je ne vois absolument rien à reprocher à la méthode de Nightmare.

Je me souviens qu'un jour, en Terminale S, on avait eu ce genre d'exo à faire. Un élève avait proposé la solution proposée par Nightmare (que j'ai aussi proposée dans un autre post où la même question a été posée), mais notre prof n'a pas trop aimé, elle a préféré écrire une suite géométrique.

Cela ne prouve rien, sauf que ton prof était peut-être vexée...parce que la méthode préconisée par Nightmare est tout simplement plus courte, plus élégante : manque de rigueur scientifique !

Pour être vraiment rigoureux, il faudrait calculer ce que cela donne pour , puis faire tendre vers

Je ne comprends pas vraiment ce que tu veux dire. L'écriture 0.457457457... signifie très exactement limite pour n tendant vers l'infini de 0.457457457...457 avec "457" écrit n fois.

C'est une question de goût à mon avis.

Oui, de goût ! Et aussi d'amour propre de celle qui n'a pas trouvé la plus belle solution et qui la dénigre pour sauver la face devant ses élèves...

Mais bon. Tout cela n'est pas très important. Honnêtement, j'aurais bien voulu penser tout seul à la méthode de Nightmare. Cela dit, pour moi les séries géométriques, c'est facile de chez facile ; mais je reconnais que cela peut être moins facile pour un lycéen... et c'est pour cela que j'aurais dû proposer la méthode de Nightmare...

:++:

[phenomene]

Pffff, bien évidemment, la prof connaissait la méthode de Nightmare et n'a pas réagi par jalousie. Mais cette méthode n'est pas rigoureuse, précisément parce qu'écrire 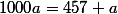à partir de l'écriture décimale illimitée de relève d'un tour de passe-passe : c'est supposer a priori que les règles de calcul sur les nombres décimaux s'appliquent aux nombres dont l'écriture décimale est illimitée, ce qui n'a rien d'évident (ces calculs demanderaient un nombre infini d'opérations ! or une démonstration se doit d'être de longueur finie).
Pour définir rigoureusement l'écriture décimale illimitée d'un réel (ici d'un rationnel), on utilise la notion de série, et sur les séries, on peut calculer proprement.

Maintenant, on peut considérer la preuve de Nightmare comme une version vulgarisée de celle avec les séries (conceptuellement, c'est en effet le même argument). Et c'est évidemment cette preuve qu'il faut présenter à un élève de seconde !

[Nightmare]

Oui c'est un peu comme la preuve du 0,9999...=1 :lol3:

[Anonyme]

salut je voudaris savoir comment faire cette operation:5puissance321 avec ma calculette merci

[Nightmare]

Tu vas poster ta question dans tout les posts du forum ? :triste:

[phenomene]

Peux-tu estimer l'ordre de grandeur du nombre que tu proposes ? Sais-tu quel est le plus grand nombre que peut traiter ta calculatrice ? Ses capacités ne sont pas illimitées...

[Chimerade]

Pffff, bien évidemment, la prof connaissait la méthode de Nightmare et n'a pas réagi par jalousie. Mais cette méthode n'est pas rigoureuse, précisément parce qu'écrire à partir de l'écriture décimale illimitée de relève d'un tour de passe-passe : c'est supposer a priori que les règles de calcul sur les nombres décimaux s'appliquent aux nombres dont l'écriture décimale est illimitée, ce qui n'a rien d'évident (ces calculs demanderaient un nombre infini d'opérations ! or une démonstration se doit d'être de longueur finie).
Pour définir rigoureusement l'écriture décimale illimitée d'un réel (ici d'un rationnel), on utilise la notion de série, et sur les séries, on peut calculer proprement.

Maintenant, on peut considérer la preuve de Nightmare comme une version vulgarisée de celle avec les séries (conceptuellement, c'est en effet le même argument). Et c'est évidemment cette preuve qu'il faut présenter à un élève de seconde !

Tu as le droit d'en penser ce que tu veux. Mais je ne partage pas ton opinion. Désolé !

[phenomene]

Tu as le droit d'en penser ce que tu veux. Mais je ne partage pas ton opinion. Désolé !

Désolé mais les mathématiques ne sont pas une question d'opinion. L'écriture décimale illimitée d'un réel est une manière "abrégée" pour parler de la somme d'une série. Comme tu l'as remarqué, au fond, cela signifie la même chose, mais il n'est pas possible de définir rigoureusement la multiplication par mille de sans avoir conscience qu'il s'agit d'une somme de série. Il n'est tout simplement même pas possible de donner un sens rigoureux à l'écriture sans parler de limite. Alors oui, la preuve de Nightmare peut être rendue rigoureuse, à condition de savoir de quoi l'on parle (Nightmare n'est pas en cause hein, lui il sait), et cela revient à manipuler des séries. Au fond, les preuves sont presque les mêmes, mais l'une n'est pas explicitée à fond, ce qui la fait à tort apparaître plus courte et astucieuse.

Quant à affirmer qu'un professeur de mathématiques ignore le raisonnement de Nightmare, c'est très mal connaître le niveau de culture mathématique de n'importe quel professeur ! Tout le monde sait ça... En revanche, il est probable que le professeur en question a voulu que l'utilisation de limites soit clairement visible dans la démonstration et non masquée derrière de mystérieux points de suspension.De plus, il s'agissait probablement de donner une application de la somme d'une série géométrique, pour illustrer le cours sur le sujet.