Problème première partie

[RAI|)EN]

Salut à tous,
voilà je bloque sur un exo en math voici la première partie de l'énoncé

1) Dans un repère ortho normal direct, soit A le point de coordonné (1 ;0), téta la droite d’équation x=1 et T le cercle de centre A et de rayon 1.

a) Soit d la droite d’équation y=tx avec t réel positif ; on appelle I1 et I2 et les point d’intersection de d avec téta et avec T. exprimer en fonction de t les coordonnées de I1 et I2

b) Soit m le point tel que vecteur OM = vecteur I1I2 . exprimer en fonction de t les coordonner de x et y de M

c) Exprimer t en fonction de l’abscisse x de M, puis démontrer que
y= x ;)(1-x)/(1+x)

pour la a) je trouve I1 (1;1/t) et pour I2 je sais pas

merci pour vos réponse

[Ericovitchi]

non I1 c'est l'intersection de la droite x=1 avec la droite y=tx
donc x=1 et y=t et pas 1/t

Pour I2 il faut remarquer que l'angle au centre que forme AI2 avec l'axe des X est le double de AOI1

Si AOI1 vaut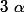 (on a ) ,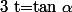
l'abcisse de I2 = OA + AI2 cos 2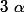 = 1+ cos 2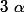
l'ordonnée de I2 = AI2 sin 2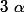 =sin 2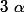

Après il faut connaître ses formules de trigo qui donne Cos 2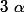 et sin 2 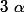en fonction de Tan 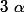donc t

[RAI|)EN]

je comprend pas comment tu détermine l'abcisse te l'ordonner de I2

[Ericovitchi]

Tu projettes sur ox et oy cette expression en sachant que l'angle
ce qui revient à remplaçer par les coordonnées et

Ca donne

[RAI|)EN]

D'accord :id: , et comment on fait pour l'exprimer en fonction de t, on se sert d'une relation sin, cos et tan car on sait que t=tan a ? par contre je ne me souviens pas de la relation si elle existe. Est ce que ce serait :
tanx=sinx/cosx

[Ericovitchi]

je te l'ai déjà dit, il faut connaître ses formules de trigo.

[RAI|)EN]

merci mais je comprend pas comment tu fait