[FONT=Comic Sans MS]Bonjour,
Voici un problème qui nous à été donné par notre prof, après plusieurs réflexions nous ne trouvons aucune solutions... Notre prof nous a éclairé sur le sujet en nous donnant une piste: mises en Équations
Si vous avez des conseils ou aides à nous donner ! :id:
On dispose d'une pizza pour 5 personnes de 50*30cm (rectangulaire) qui a de la croûte sur seulement 2 côtés adjacents,
Cette pizza doit être:
- Coupée en 5 parts et en 4 coups de couteau (en coupant droit)
- Chaque part doit avoir la même aire
- Chaque personne doit avoir autant de croûte que les autres
De quelle manière doit-on découper cette pizza ? :help:
[/FONT]
Problème: "La Pizza rectangulaire"
11 messages
- Page 1 sur 1
Chaque part doit avoir la même aire
tu connais l'aire totale, tu sais la diviser par 5 tu connais en conséquence l'aire de chaque part
Chaque personne doit avoir autant de croûte que les autres
50+30=80, tu sais diviser par 5, tu connais en conséquence la longueur de croûte de chacun
essaie de continuer
tu connais l'aire totale, tu sais la diviser par 5 tu connais en conséquence l'aire de chaque part
Chaque personne doit avoir autant de croûte que les autres
50+30=80, tu sais diviser par 5, tu connais en conséquence la longueur de croûte de chacun
essaie de continuer
vraiment ?
on va appeler ABCD la pizza complète avec les côtés [AB] et [BC] en croûte
tu connais les points sur la croûte où le couteau coupe : partant de A, on trouve M (sur le côté [AB]) puis N, P et Q sur le côté [BC]
comme on n'a droit qu'à 4 coups de couteau, et qu'on a déjà 4 points, obligatoirement l'autre point de coupe détermine le tracé
la part qui contient A et M est donc triangulaire, le 3ème point est donc sur [AD] et la part triangulaire ; soit M' ce point, il est parfaitement défini par l'aire de la part (et tu devrais le trouver à 37,5 cm de A)
de la même manière la part qui contient C et Q contient aussi D, cette part est donc un trapèze et le point Q' sur [AD] (tu devrais trouver Q'D=4 cm)
je te laisse continuer pour déterminer P' et N' sur [AD], pense à l'aire d'un trapèze quelconque
on va appeler ABCD la pizza complète avec les côtés [AB] et [BC] en croûte
tu connais les points sur la croûte où le couteau coupe : partant de A, on trouve M (sur le côté [AB]) puis N, P et Q sur le côté [BC]
comme on n'a droit qu'à 4 coups de couteau, et qu'on a déjà 4 points, obligatoirement l'autre point de coupe détermine le tracé
la part qui contient A et M est donc triangulaire, le 3ème point est donc sur [AD] et la part triangulaire ; soit M' ce point, il est parfaitement défini par l'aire de la part (et tu devrais le trouver à 37,5 cm de A)
de la même manière la part qui contient C et Q contient aussi D, cette part est donc un trapèze et le point Q' sur [AD] (tu devrais trouver Q'D=4 cm)
je te laisse continuer pour déterminer P' et N' sur [AD], pense à l'aire d'un trapèze quelconque
Pblmaths14 a écrit:Oui, on a trouver 300cm2 par personne et 16cm de croûte par personne mais après on ne sait pas comment faire on a essayer des schémas, découpages... On ne trouve pas!
Merci el niala
Et bien tu découpes dans le sens de la longueur, bien sûr : d'une croûte à l'autre comme tu ferais à la maison :ptdr:
Et tu n'as besoin que de 4 coups de couteau pour faire 5 parts.
Je crois que vous avez un prof facécieux pour avoir prétendu qu'il fallait mettre en équation.
pas très clair, il suffit juste de connaître l'aire d'un trapèze de côtés parallèles de longueur L et l et de "hauteur" h, alors :
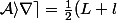\times h)
d'où ici\times DC)
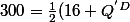\times 30)
d'où le résultat
pour les 2 parts suivantes, tu devrais trouver la même chose pour P'Q' et N'P'
et ce n'est pas la peine de vérifier l'aire de la dernière part :zen:
d'où ici
d'où le résultat
pour les 2 parts suivantes, tu devrais trouver la même chose pour P'Q' et N'P'
et ce n'est pas la peine de vérifier l'aire de la dernière part :zen:
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
