Probleme avec Caractérisation de la colinéarité dans une base.

[Le dechu des math]

Bonjours a tous.
Je suis en seconde et j'ai un niveau entre le faible et le moyen.
Aujourd'hui , en cours , le prof de math a dictée la leçon et l'exemple de :"Caracterisation de la colinéarité dans une base."Cependant la vitesse du prof a dictée son cours est trop rapide pour moi , la prise de note est donc médiocre.C'est pour cela que j'aimerai que quelqun m'explique clairement la :"Caracterisation de la colinéarité dans une base"et me donne si possible un exemple.

Merci

A cause de cela ma moyenne est de 2.4 au premier trimestre , ca peut plus continuer...

[maturin]

tu as 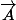colinéaire à 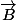si et seulement si il existe un nombre réel tel que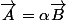


en gros si tu te le représentes graphiquement ça veut dire qu'ils ont même direction (qu'ils sont "sur la même ligne")

enfin ça c'est plus la définition qu'une caractérisation...

et aussi c'est vrai pour des vecteurs non nuls.
Je sais pas si on peut dire qu'un vecteur nul est colinéaire à un autre...

[Zebulon]

Bonsoir,

Je sais pas si on peut dire qu'un vecteur nul est colinéaire à un autre...

j'ai toujours appris cette convention.

[Le dechu des math]

Je le sais deja ca , c'est Caracterisation de la colinéarité dans une base
Mais merci quand meme.