Probabilités élémentaires

[yoshi13]

Bonjour à tous,

je ne sais pas comment démarrer pour un exercice:

Il y a n élèves qui passent un oral, il y a n sujet.
Vous avez tout révisé sauf un seul sujet.

Quelle position devez vous passer afin d'avoir un maximum de chance d'esquiver le seul sujet que vous ne connaissez pas??


Les formules de cours ne m'aide pas.
Et je ne vois pas en quoi la position change qqch.
Si on passe en premier, il y a une chance sur n de tirer le mauvais sujet.
Si on passe dans les derniers, même s'il reste peu de copies, il est tout aussi probable que quelqu'un d'autre ait déjà tiré le sujet qu'on a pas révisé...

Je tourne en rond, merci d'avance pour votre aide

[Ben314]

Salut,

Et je ne vois pas en quoi la position change qqch.

moi non plus...

[yoshi13]

Salut,

Et je ne vois pas en quoi la position change qqch.

moi non plus...

Hello Ben, merci pour ton message,

Si tu penses pareil que moi, et en supposons que nous voyons juste ^^

peut-être que la réponse attendue est qqch du style, les deux événements sont indépendants ou incompatibles...

enfin je dirais plutot indépendant car l evenement "je suis a telle position et je tire le mauvais sujet" existe

Il n y pas incompatibilité, juste que la probabilité de tirer le mauvais truc ne dépend pas de la position occupée...

[Ben314]

Perso, je répondrait surement pas en terme "d'évènement incompatible" vu que je vois aucun rapport entre le cas étudié et la notion "d'évènement incompatible" (rappel : ça signifie que la proba qu'ils se produisent tout les deux est nulle).
Et même le terme "indépendant", je vois pas trop ce qu'il viendrait f... ici : la question, c'est "en quelle position tu doit te placer pour avoir la plus grand proba de ..." et je vois pas bien le rapport avec une quelconque notion d'indépendance.
Si tu veut absolument utiliser un "mot technique", celui adapté à ce contexte serait plutôt celui de "équiprobable" :

Les évènements "le sujet tabou tombe en premier", "le sujet tabou tombe en second" , "le sujet tabou tombe en troisième", ... , "le sujet tabou tombe en dernier" sont équiprobables.

Et évidement, à l'autre extrémité, tu peut répondre

On s'en fout, ça change rien.

P.S. : Perso, en temps que prof., autant la réponse 2 me semble un peu "gonflée", autant la réponse 1 me semble un peu "pédante" et je préfèrerais un compromis : pas de l'argot, mais pas du "jargon technique" là où c'est pas vraiment utile, ou alors avec ensuite une vrai phrase en Français que tout le monde peut comprendre.

[Al-Kashi]

Quelques indications:
On note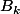 l'événement: "le sujet tiré est celui sur lequel le candidat a fait l’impasse" et on pose .

1) Calculer .
2) Montrer que et calculer .
3) Montrer que et calculer .
4) Calculer . Y a-t-il un rang de passage préférentiel pour le candidat ?

[beagle]

Je l'aurais posé autrement ce problème.
Tu peux choisir le moment de te présenter, et en plus tu sais en demandant à celui qui sort, tu sais quel sujet il a tiré.
Faut-il attendre que le sujet impasse soit tiré et se présenter ensuite,
ou bien c'est pareil, je rentre quand je veux.

[Ben314]

Ca ne change rien et, a mon sens, il n'est pas utile (voire c'est même néfaste) de faire un quelconque calcul.

Mais en fait, en réfléchissant un peu plus, le fait de faire ou ne pas faire des calculs dépend de la façon dont on interprète l'énoncé qui (comme à peu prés toujours en proba.) est flou :
L'énoncé ne précise rien concernant la façon dont les différents sujets sont tirés donc on peut se poser les questions suivantes :

1) Les différents tirages (quelque soient leurs modalités) sont ils équiprobables ?
Le bon sens nous dicte de considérer que OUI, vu que ça semble plus que plausible "concrètement parlant" et qu'en plus, si ce n'était pas le cas, il serait totalement impossible de répondre à une quelconque question.

2) Y-a-t-il tirage "avec remise" ou bien "sans remise", c'est à dire, lorsqu'un sujet a été tiré par un élève, est-il ou pas remis dans la liste des sujets possible pour l'élève suivant ?
Là, le bon sens nous dit que c'est sans doute "sans remise" vu que sinon, l'exercice serait réellement très stupide : ça serait exactement la même expérience reproduite à chaque candidat donc les même proba.

3) Arrivé à ce point, tout n'est pas encore très clair vu qu'il y a deux façon de voir ce "tirage sans remise et équiprobable" :
- Soit sous la forme d'une urne où on enlève les boules les unes après les autre et donc en recommençant à chaque fois une expérience aléatoire avec de moins en moins de boules (=on présente les sujets restant au candidat et il choisi au hasard avec équiprobabilité)
Et là, effectivement, il peut éventuellement y avoir un (vague) calcul à faire pour montrer que la proba de tirer la boule N° 1 (par exemple) au premier tirage est la même que de la proba de la tirer au 2em tirage etc...
- Soit les sujets sont mélangés au départ puis disposés en pile (avec factorielle(N) ordres possible pour la pile et équiprobabilité des différents ordres) puis le premier candidat prend le premier sujet de la pile, le second prendra le 2em sujet, etc...
Et avec ce point de vue là, à mon sens, il n'y a aucun calculs à faire : l'équiprobabilité des différents "ordres" nous donne immédiatement l'équiprobabilité concernant la position d'un sujet dans la pile.
Tout au plus et à la rigueur, on peut faire un mini dénombrement pour vérifier que Cas_favorable/Cas_total=factorielle(N-1)/factorielle(N)=1/N dans tout les cas.

[beagle]

Bonjour Ben314,
je ne peux qu'acquiesser.

Sur le mot clé équiprobabilité que tu avais donné dès le début et que tu redéveloppes.

Perso je faisais quand même ton calcul final (n-1)! / n!

et c'est en faisant ce calcul que j'ai réussi à m'embrouiller l'esprit avec mais si je sais ce qui est sorti, vais-je faire apparaître de la proba conditionnelle qui change le problème.
Il m'a semblé sans recalculer à fond, mais il me semblait bien que cela ne changeait rien.
Donc je me disais peut-être que cela faisait plus d'embrouilles.

[Ben314]

Sur le plan pédagogique, je sais pas si c'est super judicieux au niveau Lycée de montrer qu'il y a deux "modélisations" concernant un tirage aléatoire sans remise : j'ai l'impression que dans bon nombre d'exo. (voire dans le cours), on adopte le point de vue "le plus adapté" en considérant comme "évident" que les deux modélisations donnent les mêmes résultats.

[yoshi13]

Bonjour à tous et merci pour vos messages

Je poserai la question à mon prof de proba la semaine prochaine et reviendrai vous dire ce qu'il en est.

C'est un exercice d'un td de licence math, mais comme dans l ensemble du td les exos sont "préliminaires", je l'ai mis dans la section "lycée".

De mon côté je pense comme vous, la position importe peu, je ne vois pas de facon d'augmenter ses chances d'equiver le sujet non révisé.

Il s'agit bien d'un "tirage sans remise" et on ne peut pas demander aux étudiant qui sortent de la salle quel sujet ils ont eu.

[beagle]

Bah déjà Ben314 a épuisé tous les cas de figure, donc on attend rien de la solution.

Les ordres de passages 1 à n sont en bijection avec les n sujets,
il s'agit donc des permutations des sujets, soit n!
lorsqu'on identifie la place d'un sujet donné, il peut ètre à n places et pour chaque place donnée il pourra correspondre à (n-1)! permutations des sujets connus ,
et ceci quel que soit l'emplacement, donc une proba identique partout = c'est l'equiproba.

[yoshi13]

Quelques indications:
On note l'événement: "le sujet tiré est celui sur lequel le candidat a fait l’impasse" et on pose .

1) Calculer .
2) Montrer que et calculer .
3) Montrer que et calculer .
4) Calculer . Y a-t-il un rang de passage préférentiel pour le candidat ?

Merci pour ton message Al-Kashi

P(B1) = 1/n

on voit bien que les evenements B1 et B2 étant incompatibles, ils sont disjoints donc B2 inclus dans B1 complémentaire, ainsi de suite

En réitérant les possibilités je finis avec du (n-1)!/n! = 1/n

Donc le rang importe peu

[yoshi13]

Bah déjà Ben314 a épuisé tous les cas de figure, donc on attend rien de la solution.

Les ordres de passages 1 à n sont en bijection avec les n sujets,
il s'agit donc des permutations des sujets, soit n!
lorsqu'on identifie la place d'un sujet donné, il peut ètre à n places et pour chaque place donnée il pourra correspondre à (n-1)! permutations des sujets connus ,
et ceci quel que soit l'emplacement, donc une proba identique partout = c'est l'equiproba.

Okok,

en tout cas merci à tous pour votre temps

[Al-Kashi]

Bah déjà Ben314 a épuisé tous les cas de figure, donc on attend rien de la solution.

Les ordres de passages 1 à n sont en bijection avec les n sujets,
il s'agit donc des permutations des sujets, soit n!
lorsqu'on identifie la place d'un sujet donné, il peut ètre à n places et pour chaque place donnée il pourra correspondre à (n-1)! permutations des sujets connus ,
et ceci quel que soit l'emplacement, donc une proba identique partout = c'est l'equiproba.

Okok,

en tout cas merci à tous pour votre temps

Dans ce genre de situations, il serait intéressant d'étudier les cas pour avoir une première idée puis généraliser si c'est possible .

[beagle]

Bon alors comme toujours il ya plusieurs méthodes de résolution.
Et comme souvent résoudre un problème c'est se ramener à un schéma , une matrice déjà connue et plaquer la situation actuelle dessus.
Donc lorsque je découvre ce problème mon esprit part sur un truc, celui de Ben314 part sur un autre schéma et chaque personne idem.

Donc perso, et ce n'était pas le plus malin(Mais quand c'est facile tu ne cherches pas à faire du plus facile,aux échecs dès que tu trouves une série de coups qui mènent à la victoire tu es tenté de jouer directement cela sans chercher du encore plus joli, encore plus rapide).Donc je prends l'exo et pour moi on joue à quoi?
J'ai des numéros 1 à n qui sont l'ordre d'apparition, j'ai des lettres qui sont les sujets.Et un évènement élémentaire est associer 1à d, 2 à f, 3 à b etc...
Donc je me dis ben alors les évènements c'est de classer avec ordre les sujets, un évènement est (t,k, j, l,m...,d)
Bref toutes les combis ben c'est permutation des n sujets.
Pour un emplacement du sujet i comme impasse, ben je le mets à un emplacement, et le nombre de combi que j'ai (évènements favorables ) c'est les permutations de n-1 donc (n-1)!
proba que i soit emplacement quel qu'il soit est idem (n-1)!/(n!

alors c'est vrai que si tu réfléchis c'est pas le plus simple.Car il s'agit, plus basiquement ,de façon binaire de mettre 1 pour un sujet connu et mettre le 0 pour le sujet impasse.Bref je place le 0 dans un des n emplacements possibles.C'est équiprobable qu'il soit aux différents emplacements.Donc tomber sur le 0 sera de 1/n.
En fait si on se ramène à du basique de débutant.C'est un jeu de cartes.je dois sortir (ou je ne veux pas sortir )une carte donnée.Ben que je sois obligé de prendre la carte du dessus du paquet, que je sois obligé de prendre la septième carte, que j'ai le choix libre de prendre une carte au hasard (équivalent à je choisis quand rentrer dans l'examen), ben tout cela ne change en rien et c'est une chance sur l'ensemble des cartes du jeu.Je pense que lorsque Ben314 arrive sur un tel sujet il voit le problème de façon aussi basique que cela et donc il dit vous allez calculer quoi? c'est de l'équiproba et terminé.

[Ben314]

J'ai effectivement dit au début qu'a mon sens "c'était pas malin" de faire un quelconque calcul, mais ce que je raconte dans mon (long) post., au fond, ça dit que c'est pas si clair que ça qu'il ne faut rien écrire du tout (comme quoi...)
En fait, à mon sens, le problème c'est de savoir, lorsque tu doit "tirer au hasard un ordre pour les entier 1 à 5", tu peut :
1) Mettre 5 boules dans une urne, les tirer l'une après l'autre (sans remise) et noter comme "résultat de l'expérience" l'ordre dans lesquelles tu les as tiré.
2) Écrire sur une feuille la liste des 5!=120 ordres possible puis tirer une boule N dans une urne en contenant 120 numéroté de 1 à 120 et prendre comme "résultat de l'expérience" la N-ième permutation de la liste.

Dans le cas 1), on peut effectivement faire des calculs pour déterminer la proba de tirer la 1 en premier (=1/5), de la tirer en second (=4/5x1/4=1/5) en troisième (=4/5x3/4x1/3=1/5), etc...
Mais on peut aussi montrer (ou savoir ou admettre) que les modélisations 1) et 2) donnent la même proba pour les différents permutations (en montrant que dans le cas 1) tout les tirages sont équiprobables) et constater que, dans le cas 2), il n'y a rien à calculer tellement l'équiprobabilité des différentes positions pour le 1 est claire (par symétrie du problème)

[beagle]

Il me semble que calcul ou pas calcul dépend uniquement de la rédaction de la solution proposée et dépend uniquement du modèle utilisé par analogie au problème.(et bien sur à l'acceptation de ce modèle comme représentant bien l'énoncé).
Donc si je dis je note 1 lorsque je tombe sur un sujet connu et je note 0 lorsque je tombe sur le sujet impasse.
Il s'agit alors d'une série de n-1 fois le 1, avec un 0 à placer.
Ce 0 est d'emplacement équiprobable dans la série.
Lorsqu'on me donne un numéro ou bien lorsque je choisis mon ordre de passage, je choisis ou bien on m'impose aléatoirement un emplacement.Donc je suis bien en équiprobabilité de tomber sur le zéro.
Le problème est identique à trouver une carte dans un jeu, la proba est la même si je prends la carte au-dessus du paquet que de prendre une carte choisie au hasard.

Bon c'est un peu long comme rédaction.Je ne sais pas si mettre les calculs cela ne va pas plus vite