Salut tout le monde !
J'ai fini mes études et je me suis replongé récemment dans le monde des probabilités... Sauf que mes cours sont enfouis dans ma mémoire. J'ai bien essayé via youtube de revenir dedans mais pour mon problème, les arbres de probabilité ça va pas le faire sur 12tirages et une condition qui m'énerve! ( Ou alors il me faut une très grande feuille )
J'ai un paquet de 12 cartes avec remise
6 cœurs (rouge)
3 piques (noir)
2 trèfle (noir)
1 carreaux (rouge)
Sur 12 tirages successifs avec remise, quelle est la probabilité d'avoir plus de carte rouges que de noire sans jamais tomber sur du trèfle ?
Si quelqu'un pouvait me guider ce serait sympa !
Probabilités Bernoulli et condition
3 messages
- Page 1 sur 1
Re: Probabilités Bernoulli et condition
L'univers : c'est tous les tirages possibles. Il y a  tirages possibles.
tirages possibles.
Parmi ces tirages, on va déjà compter les tirages qui ne contiennent aucun trèfle :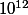
Si le seul critère était : n'avoir aucun trèfle, on aurait donc une probabilité^{12}=0.112)
L'autre condition est d'avoir plus de cartes rouges que de cartes noires.
Les 2 conditions sont indépendantes. On peut considérer qu'on travaille maintenant avec un jeu de 10 cartes (6 coeurs, 3 piques, 1 carreau) , on tire (avec remise) 12 cartes, et on veut la probabilité d'avoir plus de rouges que de noirs.
Proba d'avoir 12 rouges =^{12})
Proba d'avoir 11 rouges =*(7/10)^{11})
Proba d'avoir 10 rouges =/2* (3/10)^2*(7/10)^{10})
Proba d'avoir 9 rouges =/(2*3)* (3/10)^3*(7/10)^{9})
Proba d'avoir 8 rouges =/(2*3*4)* (3/10)^4*(7/10)^{8})
Proba d'avoir 7 rouges =/(2*3*4*5)* (3/10)^5*(7/10)^{7})
Si on additionne ces différentes probabilités, on obtient 0.882.
Par sécurité, pour controle, on calcule aussi les probas d'avoir 6 cartes rouges, 5 cartes rouges , etc ... la somme de toutes les probabilités doit donner 1, sinon, on s'est planté quelque part !
Il faut donc multiplier ces 2 résultats : P = 0.882*0.112 =0.09894
Parmi ces tirages, on va déjà compter les tirages qui ne contiennent aucun trèfle :
Si le seul critère était : n'avoir aucun trèfle, on aurait donc une probabilité
L'autre condition est d'avoir plus de cartes rouges que de cartes noires.
Les 2 conditions sont indépendantes. On peut considérer qu'on travaille maintenant avec un jeu de 10 cartes (6 coeurs, 3 piques, 1 carreau) , on tire (avec remise) 12 cartes, et on veut la probabilité d'avoir plus de rouges que de noirs.
Proba d'avoir 12 rouges =
Proba d'avoir 11 rouges =
Proba d'avoir 10 rouges =
Proba d'avoir 9 rouges =
Proba d'avoir 8 rouges =
Proba d'avoir 7 rouges =
Si on additionne ces différentes probabilités, on obtient 0.882.
Par sécurité, pour controle, on calcule aussi les probas d'avoir 6 cartes rouges, 5 cartes rouges , etc ... la somme de toutes les probabilités doit donner 1, sinon, on s'est planté quelque part !
Il faut donc multiplier ces 2 résultats : P = 0.882*0.112 =0.09894
Re: Probabilités Bernoulli et condition
on doit pouvoir le faire directement avec une pseudo loi binomiale où p et q ne sont plus q=1-p
Quant à etre perdu dans l'arbre de proba,
c'est justement tout l'intérèt de l'apprentissage des coefficients binomiaux et de se dire que dans un arbre on peut avoir des séquences de meme proba en changeant juste l'ordre des branches ...
Dans un arbre de proba si tu vois proba p et proba q qui se succèdent ainsi:
pxpxq p xq
ce sera idem en proba que la succession de probas:
qxqxpxpxp
tout cela sera de proba: q²xp^3
et si tu veux compter ensemble tous ces évènements
et bien tu vas additionner toutes les combinaisons de placer q dans deux emplacements sur 5 emplacements
C(5,2) qui est idem à placer les 3 p dans 5 emplacements le C(5,3)
donc tu feras
C(5,2)xq²xp^3
donc tout plein de branches, ne prends pas la machette pour avancer, suffit de les regrouper, toutes celles qui sont pareils sont de proba truc:( p^h x q^j) et j'en ai combinaisons machin C(n,k) ...
Quant à etre perdu dans l'arbre de proba,
c'est justement tout l'intérèt de l'apprentissage des coefficients binomiaux et de se dire que dans un arbre on peut avoir des séquences de meme proba en changeant juste l'ordre des branches ...
Dans un arbre de proba si tu vois proba p et proba q qui se succèdent ainsi:
pxpxq p xq
ce sera idem en proba que la succession de probas:
qxqxpxpxp
tout cela sera de proba: q²xp^3
et si tu veux compter ensemble tous ces évènements
et bien tu vas additionner toutes les combinaisons de placer q dans deux emplacements sur 5 emplacements
C(5,2) qui est idem à placer les 3 p dans 5 emplacements le C(5,3)
donc tu feras
C(5,2)xq²xp^3
donc tout plein de branches, ne prends pas la machette pour avancer, suffit de les regrouper, toutes celles qui sont pareils sont de proba truc:( p^h x q^j) et j'en ai combinaisons machin C(n,k) ...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
